Trapezoidal Method

C Program

A number of definite integrals need to be solved in applied mathematics, physics and engineering. The manual analytical solution of definite integrals is quite cumbersome and time consuming. So, in this post I have presented source code in C program for Trapezoidal method as one of the computer-programming-based solutions of definite integrals. The techniques of numerical methods are used to solve this equation; it involves a number of calculations and efforts have been made to minimize error in the program.
The trapezium or trapezoidal rule can be used as a way of estimating the area under a curve because the area under a curve is given by integration. So, the trapezoidal rule gives a method of estimating integrals. This is useful when you come across integrals that you don’t know how to evaluate. So, the program for trapezoidal method in C given here is applicable to calculate finite integral or area under a curve.
The basic working principle of the trapezoidal method c program is that trapezoidal method splits the area under the curve into a number of trapeziums. Then, area of each trapezium is calculated, and all the individual areas are summed up to give the total area under the curve which is the value of definite integral.

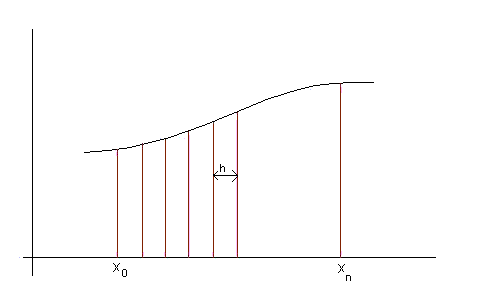
In the above figure, area under the curve between the points x0 and xn is to be determined. In order to determine the area, we divide the total interval (xn– x0) into ‘n’ small interval each of length ‘h’:

h=(xn– x0)/n

After that, the C source code for trapezoidal method uses the following formula to calculate the value of definite integral:

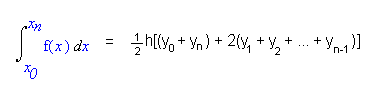
Source Code for Trapezoidal Method in C:

#include< stdio.h>
#include< conio.h>
#include< math.h>
float f(float x)
{
    return(1/(1+pow(x,2)));
}
void main()
{
    int i,n;
    float x0,xn,h,y[20],so,se,ans,x[20];
    printf("\n Enter values of x0,xn,h:\n");
    scanf("%f%f%f",&x0,&xn,&h);
    n=(xn-x0)/h;
    if(n%2==1)
    {
        n=n+1;
    }
    h=(xn-x0)/n;
    printf("\nrefined value of n and h are:%d  %f\n",n,h);
    printf("\n Y values \n");
    for(i=0; i<=n; i++)
    {
        x[i]=x0+i*h;
        y[i]=f(x[i]);
        printf("\n%f\n",y[i]);
    }
    so=0;
    se=0;
    for(i=1; i< n; i++)
    {
        if(i%2==1)
        {
            so=so+y[i];
        }
        else
        {
            se=se+y[i];
        }
    }
    ans=h/3*(y[0]+y[n]+4*so+2*se);
    printf("\nfinal integration is %f",ans);
    getch();
}

The aforementioned source code for trapezoidal method is short and simple to understand. It uses a user defined function to calculate the value of function i.e f(x) =1 /(1 + x2). The variable data type used in the program are integer and float types. There are only three variables to be input to the program – x0 ( initial boundary value), xn ( final boundary value) and h (strip length).

Input/Output:

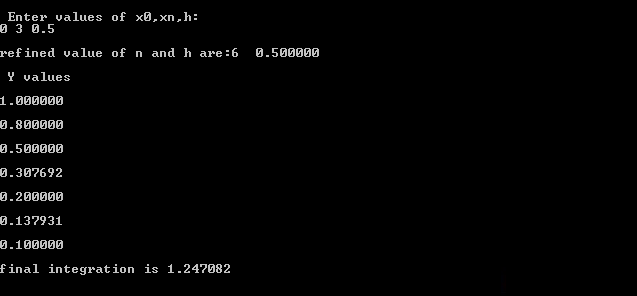
As the C program for Trapezoidal Method is executed, it asks for the value of x0, xn and h. After inputting them, it prints the refined value of n & h, and value of each ‘y’ at each intermediate points as shown in the output screen above. At the end, it prints the value of the define integral. To use this source code for other functions, just modify the return(1/(1+pow(x,2))); part in the code.

MATLAB Program

Trapezoidal method, also known as trapezium method or simply trapezoidal rule, is a popular method for numerical integration of various functions (approximation of definite integrals) that arise in science and engineering. This method is mainly applicable to estimate the area under a curve by splitting the entire area into a number of trapeziums of known area.
In this tutorial, we are going to write a program code for Trapezoidal method in MATLAB, going through its mathematical derivation and a numerical example. You can check out our earlier tutorials where we discussed a C program and algorithm/flowchart for this method.

Derivation of Trapezoidal Method:

Consider a curve f(x) = 0 as shown below:

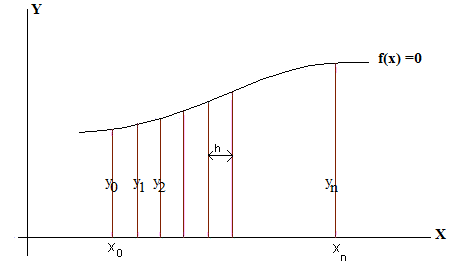
Here, the area under the curve f(x) from x0 to xn is to be determined which is theoretically nothing but the numerical integration of curve f(x) in the interval [x0, xn]. So, in order to estimate the area, we split the whole area into ‘n’ number of trapeziums or trapezoids of equal height ‘h’.
Let y0, y1, y2….. yn be the ordinates of the curve at various abscissas.

The area of first trapezium, a1 = h * (y0 +y1)/ 2
The area of second trapezium, a2 = h * (y1 +y2)
The area of third trapezium, a3 = h * (y2 +y3)/ 2
… . . . . . . . . . . . . . . . . . . . .. . . . . . . . . . . .. . .. . .
. . . .. . . . .. . . . .. . . . .. . . . . . .. .. . . . .. . . . .. . .
The area of nth trapezium, an = h * (yn-1 +yn)/ 2

The total area under the curve is the summation of all these small areas.
So, A = a1 + a2 + a3 + ….. + an
or, A= h * (y0 +y1)/ 2 + h * (y1 +y2) + h * (y2 +y3)/ 2+ ….. + h * (yn-1 +yn)/ 2
or, A= h { (y0 + yn)/2 + ( y1 + y2+ …….. + yn-1)}

Note: This formula is the required expression which will be used in the program code for Trapezoidal rule in MATLAB.

Alternatively, it can be concluded that:

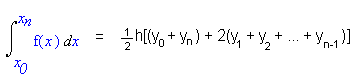
Trapezoidal Method in MATLAB:

>> n = 5; % number of small trapeziums formed after splitting 
a = 1.0; %  starting point or lower limit of the area
b = 2.0; %  end point or upper limit of the area
sum = 0.0;  % to find the sum 
dx = (b-a)/(n-1); %  to find step size or height of trapezium 
% Generating the samples 
 
for i = 1:n
    x(i) = a + (i-1)*dx; 
end
% to generate the value of function at different values of x or sample 
 
for i = 1:n
    y(i) = x(i).^2;
end
% computation of area by using the technique of trapezium method 
 
for i = 1:n
    if ( i == 1 || i == n) % for finding the sum of fist and last ordinate
        sum = sum + y(i)./2;
    else
        sum = sum + y(i); % for calculating the sum of other ordinates 
    end
end
area = sum * dx; % defining the area
 
area

The above code for Trapezoidal method in MATLAB has been programmed to find the area under the curve f(x) = x2 in the interval [1, 2]. So, the user doesn’t need to give any input to the program.
In this program, the whole area has been divided into five trapeziums. The program calculates the area of each trapezium as explained in the derivation and finds the required sum.
If it is intended to find the area under other curves using this code, the user has to change the limits and the value of the function in the source code.
To run the program, copy the given code in MATLAB command window and hit enter. Here’s a screenshot sample of the output you’ll get:

As the aforementioned MATLAB code has an inbuilt function, it may be difficult (for some of you) to modify the source code for other functions and limits. In such case, you can use this program code instead:

function I = trapezoidal_f1 ( f )
% for calculating integrals using trapezoidal rule when function is known
 
 
%asking for the range and desired accuracy
 
 R= input( ' Enter the limits of integrations [ x_min, x_max]   :\n');
 tol = input(' Error allowed in the final answer should be of an order : \n');
 a= R(1,1); b = R(1,2);
 
 %initial h and n
 n = 100;
 h = (b -a )/100;
 
 %for calculating maximum of h^2 *f''(x) in the given region
 for k = 0:100
        x( 1, k+1 ) = a +  k*h ;
        y2 ( 1, k+1) = feval ( f, x(1,k+1) + 2*h ) - 2*feval( f, x(1,k+1) + h ) + feval( f, x(k+1) );
 end 
 [ y i ] =  max( y2);
 x_opt = x(1,i);
   
 % for calculating the desired value of h
 m=0;
 while abs((feval ( f, x_opt + 2*h ) - 2*feval(f,  x_opt+ h) + feval(f, x_opt)) * ( b-a)/12) > tol % Global error for trapezoidal rule
                m = m +1;
                h = h * 10^-m;
 end
 
 %calculating  n
 n = ceil( (b-a)/h );
 h = ( b-a )/ n;
 
 % forming matrix X
 for k = 1:(n+1)
    X(k,1) = a + (k-1)*h;
    X(k,2) = feval( f, X(k,1));
 end
 
% trapezoidal formula
 
I = h/2 * (2*sum( X(:,2))- X(1,2)- X( n,2));
 % displaying final result
 h 
 n
 disp(sprintf(' The area under this curve in the interval ( %10f , %10f )  is %10.6f .',a,b,I)

When this MATLAB program is executed, it asks for the value of the interval in which the area of curve is to be estimated. After that, the user needs to input allowed error in calculation. Finally, the area under the curve is displayed as output.

To run the code, follow these steps:

• Copy the source code given above in MATLAB editor and save as file_ma m file.
• Create another MATLAB file in the same folder in which .m is saved.
• In this newly created MATLAB file, define the function following the syntax given below.

1
2
function I = trapezoidal_f1 ( f )
f = x^2

The sample output of this program is given below:

Trapezoidal Method Numerical Example:

Now, let’s analyze numerically the first program for Trapezoidal method in MATLAB. We have to find the area under the curve f(x) = x2 in the interval [1, 2].

Given function, f(x) = x2
x0 = 1 and xn = 2
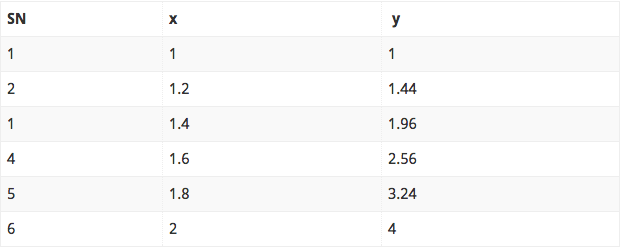
Take number of steps, n = 5 such that the height of the interval, h = ( 2-1)/5 = 0.2. Detailed calculation is presented in the table below:

Now, using the formula for trapezoidal method:
Area = 0.2/2 * [ (1+4) + 2*( 1.44 + 1.96 + 2.56 + 3.24)] = 2.3438
Thus, the answer is same as the one obtained using the program for Trapezoidal method in MATLAB.
If you have any questions regarding trapezoidal method or its MATLAB code, bring them up to me from the comments box below. Also, you can find more Numerical Methods tutorials here.

Algorithm and Flowchart

Definite integral is replica of area under a curve within the certain limit. In order to calculate such area, there have been developed a number of analytical methods but they are time-consuming, laborious and chance of occurrence of error is also high. That is why, techniques of numerical methods are very much popular in calculation numerical integration which can easily be programmed and trapezoidal method is one of them.
In this tutorial, we’re going to discuss a simple algorithm and flowchart for trapezoidal method along with a brief introduction to the method.
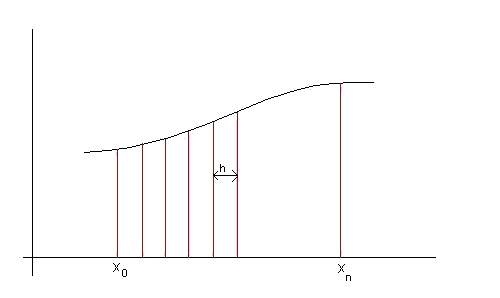
Trapezoidal method is based on the principle that the area under the curve which is to be calculated is divided into number of small segments. The bounding curve in the segment is considered to be a straight line as a result the small enclosed area becomes a trapezium.
The area of each small trapezium is calculated and summed up i.e. integrated. This idea is the working mechanism in trapezoidal method algorithm and flowchart, even it source code.
Let us consider a function f(x) representing a curve as shown in above figure. You are to find out the area under the curve from point ‘a’ to ‘b’. In order to do so, divide the distance between ab into a number vertical strips of width ‘h’ so that each strip can be considered as trapezium.

The following formula is used to calculate the area under the curve:

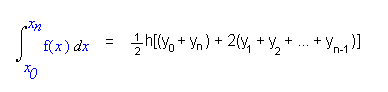
Trapezoidal Method Algorithm:

• Start
• Define and Declare function
• Input initial boundary value, final boundary value and length of interval
• Calculate number of strips, n = (final boundary value –final boundary value)/length of interval
• Perform following operation in loop
  x[i]=x0+i*h
  y[i]=f(x[i])
  print y[i]
• Initialize se=0, s0=0
• Do the following using loop
  If i %2 = 0
  So=s0+y[i]
  Otherwise
  Se=se+y[i]
• ans= h/3*(y[0]+y[n]+4*so+2*se)
• print the ans
• stop

Trapezoidal Method Flowchart:

Among a number of methods for numerical integration, trapezoidal method is the simplest and very popular method which works on the principle of straight line approximation. I hope the algorithm and flowchart presented here will guide you to write source code for the method in any high level language.