Solution of Laplace Equation

C Program

A number of potential functions need to be solved in applied mathematics, physics and engineering, and whenever the problems involving potential function come, there exists Laplace equation which is of elliptical type.
The manual analytical solution of Laplace equation is quite cumbersome and time consuming. As programming approach, here is a source code in C program for solution of Laplace equation. The techniques of numerical methods are used to solve this equation, and it involves a number of calculations; efforts have been made to minimize error.
The Laplace Equation has been derived on the consideration that, a heated plate is insulated everywhere except at its edges where the temperature is constant. Assuming that, the plane of plate coincides with xy-plane, the quantity of heat entering the face of plate in time Δt is calculated.
Developed by Pierre-Simon Laplace, the Laplace equation is defined as:
δ 2u/ δx2 + δ 2u/ δy2 = 0
The program below for Solution of Laplace equation in C language is based on the finite difference approximations to derivatives in which the xy-plane is divided into a network of rectangular of sides Δx=h and Δy=k by drawing a set of lines.
x=ih, i=0,1,2,…
y=jk, j=0, 1, 2….
The points of intersection of these families of lines are called mesh points, lattice points or grid points.
The C program for Laplace equation works by following the steps listed below:

• First of all the program asks for the boundary conditions. The user has to input the value ‘u’ at various mesh points.
• After inputting the boundary condition, the program asks for the value of maximum allowed error and the maximum number iteration. The number of iteration depends on the degree of accuracy.
• The initial values of iteration are already fixed in the source code. The program executes and there are two conditions to control the number of iteration; maximum allowed error and number of maximum number of iteration. If the desired accuracy is not met with the entered number of iteration the program gives the error message.

Source Code for Solution of Laplace Equation in C:

#include< stdio.h>
#include< math.h>
#define S 4
typedef float newvar[S+1][S+1];
void entrow(int i,newvar u)
{
    int j;
    printf("\n Enter the value of u[%d,j],j=1,%d\n",i,S);
    for(j=1;j<=S;j++)
    scanf("%f",&u[i][j]);
}
void entcol(int j, newvar u)
{
int i;
printf("Enter the value of u[i,%d],""i=2,%d\n",j,S-1);
for(i=2;i<=S-1;i++)
scanf("%f",&u[i][j]);
}
void oput(newvar u, int wd, int prsn)
{
    int i,j;
    for(i=i;i<=S;i++)
    {
        for(j=1;j<=S;j++)
        printf("%d,%d,%f",wd, prsn, u[i][j]);
        printf("\n");
 
    }
}
main()
{
    newvar u;
    float mer, ar, e, t;
   int i,j,itr, maxitr;
   for(i=1;i<=S;i++)
   for(j=1;j<=S;j++)
   u[i][j]=0;
   printf("\n  Enter the Boundary Condition\n");
   entrow(1,u); entrow(S,u);
   entcol(1,u); entcol(S,u);
   printf(" Enter the allowed error and maximum number of iteration : ");
   scanf("%f%f",&ar,&maxitr);
   for(itr=1;itr<=maxitr;itr++)
   {
       mer=0;
       for(i=2;i< S-1;i++)
       {
       for(j=2;j<=S-1;j++)
       {
           t=(u[i-1][j]+u[i+1][j]+u[i][j+1]+u[i][j-1])/4;
           e=fabs(u[i][j]-t);
           if(e>mer)
           mer=e;
           u[i][j]=t;
       }
       printf(" Iteration Number %d\n",itr);
       oput(u,9,2);
       if(mer<=ar)
       {
           printf(" After %d iteration \n The solution : \n",itr);
            oput(u,8,1);
           return 0;
 
       }
   }
   printf(" Sorry! The number of iteration is not sufficient");
   return 1;
}
}

Input/Output:

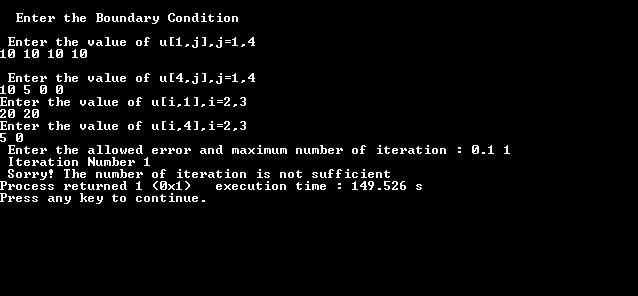
The source code is to be compiled in Code::Blocks. If you’ve any queries regarding Laplace equation or the source code, mention them in comments.