Secant Method

C Program

Secant method is the most effective approach to find the root of a function. It is based on Newton-Raphson method, and being free from derivative it can be used as an alternative to Newton’s method. The C program for Secant method requires two initial guesses, and the method overall is open bracket type. Also, the secant method is an improvement over the Regula-Falsi method as approximation is done by a secant line during each iterative operation.
The programming effort for Secant Method in C is a bit tedious, but it’s the most effective of all other method to find the root of a function. Here, at each iteration, two of the most recent approximations of the root are utilized to find out the next approximation. Also, in secant method, it is not mandatory that the interval should contain the root.
The secant method is faster than the bisection method as well as the regula-falsi method. The rate of convergence is fast; once the secant method converges, its rate of convergence is 1.62, which is quite high. Although convergence is not guaranteed in this method, this method is the most economical one giving definitely rapid rate of convergence at low cost.

• Type – open bracket
• No. of initial guesses – 2
• Convergence – super linear
• Rate of convergence – faster
• Accuracy – good
• Programming effort – tedious
• Approach – interpolation

Below is a short and simple C programming source code for Secant method to find the root of x^3 – 4 or x*x*x – 4.

Source Code for Secant Method in C:

#include< stdio.h>
float f(float x)
{
    return(x*x*x-4); // f(x)= x^3-4
}
float main()
{
    float a,b,c,d,e;
    int count=1,n;
    printf("\n\nEnter the values of a and b:\n"); //(a,b) must contain the solution.
    scanf("%f%f",&a,&b);
    printf("Enter the values of allowed error and maximun number of iterations:\n");
    scanf("%f %d",&e,&n);
    do
    {
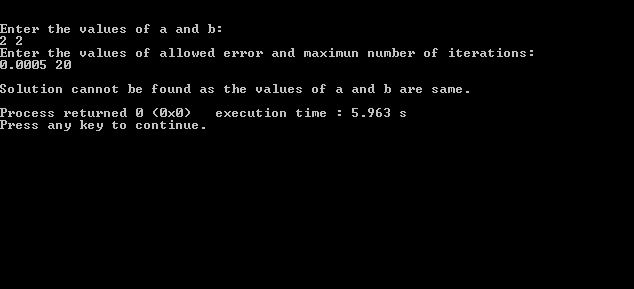
        if(f(a)==f(b))
        {
            printf("\nSolution cannot be found as the values of a and b are same.\n");
        return;
        }
        c=(a*f(b)-b*f(a))/(f(b)-f(a));
        a=b;
        b=c;
        printf("Iteration No-%d    x=%f\n",count,c);
        count++;
        if(count==n)
        {
        break;
        }
    } while(fabs(f(c))>e);
    printf("\n The required solution is %f\n",c);
 
}   

Input/Output:

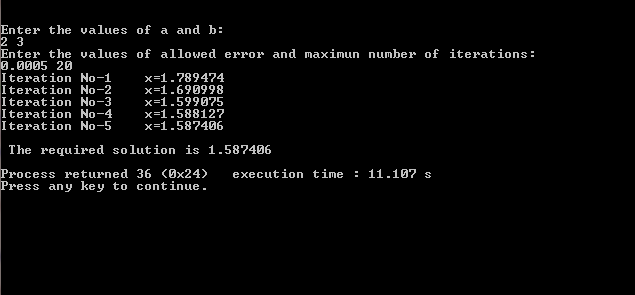
When the values for a and b, the initial guesses, are entered same, the solution can’t be obtained. In such case, enter different values for a and b such that f(a) and f(b) are not equal.

MATLAB Program

Secant method is an iterative tool of mathematics and numerical methods to find the approximate root of polynomial equations. During the course of iteration, this method assumes the function to be approximately linear in the region of interest.
Although secant method was developed independently, it is often considered to be a finite difference approximation of Newton’s method. But, being free from derivative, it is generally used as an alternative to the latter method.
Previously, we talked about secant method vis-à-vis C program and algorithm/flowchart for the method. Here, we’ll go through a program for Secant method in MATLAB along with its mathematical background and a numerical example.

Mathematical Derivation of Secant Method:

Consider a curve f(x) = 0 as shown in the figure below:

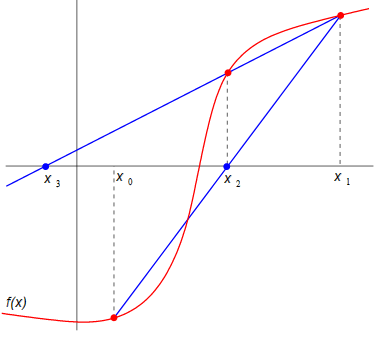
Secant method estimates the point of intersection of the curve and the X- axis (i.e. root of the equation that represents the curve) as exactly as possible. For that, it uses succession of roots of secant line in the curve.

Assume x0 and x1 to be the initial guess values, and construct a secant line to the curve through (x0, f(x0)) and (x1, f(x1)). The equation of this secant line is given by:

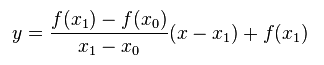
If x be the root of the given equation, it must satisfy: f(x) = 0 or y= 0. Substituting y = 0 in the above equation, and solving for x, we get:

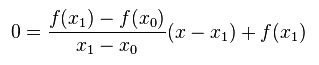
Now, considering this new x as x2, and repeating the same process for x2, x3, x4, . . . . we end up with the following expressions:

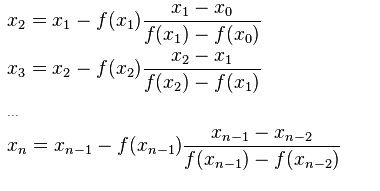
This is the required formula which will also be used in the program for secant method in Matlab.

• Its rate of convergence is more rapid than that of bisection method . So, secant method is considered to be a much faster root finding method.
• In this method, there is no need to find the derivative of the function as in Newton-Raphson method.
Limitations of Secant Method:

• The method fails to converge when f(xn) = f(xn-1)
• If X-axis is tangential to the curve, it may not converge to the solution.

Secant Method in MATLAB:

% Secant Method in MATLAB
 
a=input('Enter function:','s');
f=inline(a)
 
x(1)=input('Enter first point of guess interval: ');
x(2)=input('Enter second point of guess interval: ');
n=input('Enter allowed Error in calculation: ');
iteration=0;
 
for i=3:1000
   x(i) = x(i-1) - (f(x(i-1)))*((x(i-1) - x(i-2))/(f(x(i-1)) - f(x(i-2))));
    iteration=iteration+1;
    if abs((x(i)-x(i-1))/x(i))*100< n
        root=x(i)
        iteration=iteration
        break
    end
end 

In this program for secant method in Matlab, first the equation to be solved is defined and assigned with a variable ‘a’ using inline( ) library function. Then, the approximate guess values and desired tolerance of error are entered to the program, following the MATLAB syntax.
The program uses the secant formula (aforementioned in the mathematical derivation) to calculate the root of the entered function. Here’s a sample output of the above MATLAB code for secant method:

Secant Method Numerical Example:

Lets perform a numerical analysis of the above program of secant method in MATLAB. The same function f(x) is used here; x0 =0 and x1 = -0.1 are taken as initial approximation, and the allowed error is 0.001.

Here,
f(x) = cos(x) + 2 sin(x) + x2
x0 = 0
x1 = -0.1

For first iteration,

f(x1) = cos(-0.1) + 2 sin(-0.1) + ( -0.1 )2 = 0.8053 and
f(x0) = cos0 + 2 sin0 + 02 = 1
As we know,
x2 = x1 – f(x1)
x2 = 0 + 0.8053 * (-0.1-0)/(0.8053-1)
x2 =0.4136
Similarly, x3 = – 0.5136, and so on…
The complete calculation and iteration of secant method (and MATLAB program) for the given function is presented in the table below:

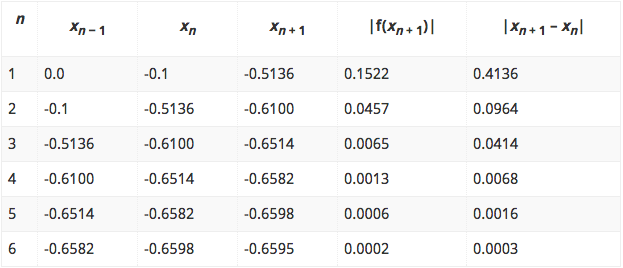
Thus, the root of f(x) = cos(x) + 2 sin(x) + x2 as obtained from secant method as well as its MATLAB program is -0.6595.
Check: f(-0.6585) = cos(-0.6585) + 2 sin(-0.6585) + (-0.6585)2 = 0.0002 (OK).
If you have questions regarding secant method or its MATLAB code, bring them up from the comments section. You can find more Numerical methods tutorial using MATLAB here .

Algorithm and Flowchart

Secant method is considered to be the most effective approach to find the root of a non-linear function. It is a generalized from the Newton-Raphson method and does not require obtaining the derivatives of the function. So, this method is generally used as an alternative to Newton Raphson method.
Secant method falls under open bracket type. The programming effort may be a tedious to some extent, but the secant method algorithm and flowchart is easy to understand and use for coding in any high level programming language.
This method uses two initial guesses and finds the root of a function through interpolation approach. Here, at each successive iteration, two of the most recent guesses are used. That means, two most recent fresh values are used to find out the next approximation.

• No. of initial guesses – 2
• Type – open bracket
• Rate of convergence – faster
• Convergence – super linear
• Accuracy – good
• Approach – interpolation
• Programming effort – tedious

Regula Falsi Method Algorithm:

• Start
• Get values of x0, x1 and e
  *Here x0 and x1 are the two initial guesses
  e is the stopping criteria, absolute error or the desired degree of accuracy*
• Compute f(x0) and f(x1)
• Compute x2 = [x0*f(x1) – x1*f(x0)] / [f(x1) – f(x0)]
• Test for accuracy of x2
  If [ (x2 – x1)/x2 ] > e, *Here [ ] is used as modulus sign*
  then assign x0 = x1 and x1 = x2
  goto step 4
  Else,
  goto step 6
• Display the required root as x2.
• Stop

Secant Method Flowchart:

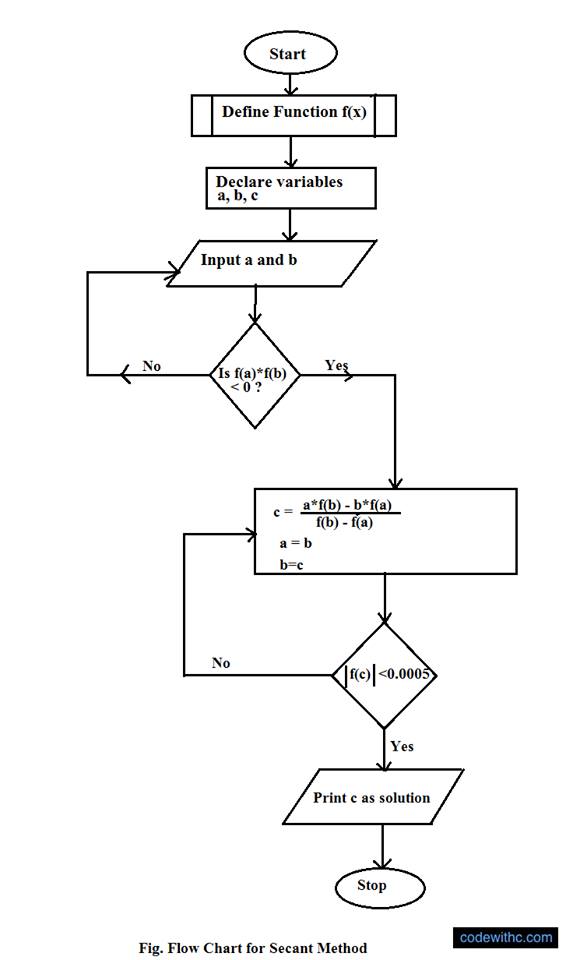
Secant method is an improvement over the Regula-Falsi method, as successive approximations are done using a secant line passing through the points during each iteration. Following the secant method algorithm and flowchart given above, it is not compulsory that the approximated interval should contain the root.
Secant method is faster than other numerical methods, except the Newton Raphson method. Its rate of convergence is 1.62, which is quite fast and high. However, convergence is not always guaranteed in this method. But, overall, this method proves to be the most economical one to find the root of a function.