Gauss Elimination Method

C Program

In engineering and science, the solution of linear simultaneous equations is very important. Different analysis such as electronic circuits comprising invariant elements, a network under steady and sinusoidal condition, output of a chemical plant and finding the cost of chemical reactions in such plants require the solution of linear simultaneous equations.
In Gauss-Elimination method, these equations are solved by eliminating the unknowns successively. The C program for Gauss elimination method reduces the system to an upper triangular matrix from which the unknowns are derived by the use of backward substitution method.
Pivoting, partial or complete, can be done in Gauss Elimination method. So, this method is somewhat superior to the Gauss Jordan method . This approach, combined with the back substitution, is quite general. It is popularly used and can be well adopted to write a program for Gauss Elimination Method in C.

For this, let us first consider the following three equations:

a1x + b1y + c1z = d1
a2x + b2y + c2z = d2
a3x + b3y + c3z = d3

Assuming a1 ≠ 0, x is eliminated from the second equation by subtracting (a2/ a1) times the first equation from the second equation. In the same way, the C code presented here eliminates x from third equation by subtracting (a3/a1) times the first equation from the third equation.

Then we get the new equations as:

a1x + b1y + c1z = d1
b’2y + c’2z = d’2
c’’3z = d’’3

The elimination procedure is continued until only one unknown remains in the last equation. After its value is determined, the procedure is stopped. Now, Gauss Elimination in C uses back substitution to get the values of x, y and z as:

z= d’’3 / c’’3
y=(d’2 – c’2z) / b’2
x=( d1- c1z- b1y)/ a1

Source Code for Gauss Elimination Method in C:

#include< stdio.h>
int main()
{
    int i,j,k,n;
    float A[20][20],c,x[10],sum=0.0;
    printf("\nEnter the order of matrix: ");
    scanf("%d",&n);
    printf("\nEnter the elements of augmented matrix row-wise:\n\n");
    for(i=1; i<=n; i++)
    {
        for(j=1; j<=(n+1); j++)
        {
            printf("A[%d][%d] : ", i,j);
            scanf("%f",&A[i][j]);
        }
    }
    for(j=1; j<=n; j++) /* loop for the generation of upper triangular matrix*/
    {
        for(i=1; i<=n; i++)
        {
            if(i>j)
            {
                c=A[i][j]/A[j][j];
                for(k=1; k<=n+1; k++)
                {
                    A[i][k]=A[i][k]-c*A[j][k];
                }
            }
        }
    }
    x[n]=A[n][n+1]/A[n][n];
    /* this loop is for backward substitution*/
    for(i=n-1; i>=1; i--)
    {
        sum=0;
        for(j=i+1; j<=n; j++)
        {
            sum=sum+A[i][j]*x[j];
        }
        x[i]=(A[i][n+1]-sum)/A[i][i];
    }
    printf("\nThe solution is: \n");
    for(i=1; i<=n; i++)
    {
        printf("\nx%d=%f\t",i,x[i]); /* x1, x2, x3 are the required solutions*/
    }
    return(0);
}   

Input/Output:

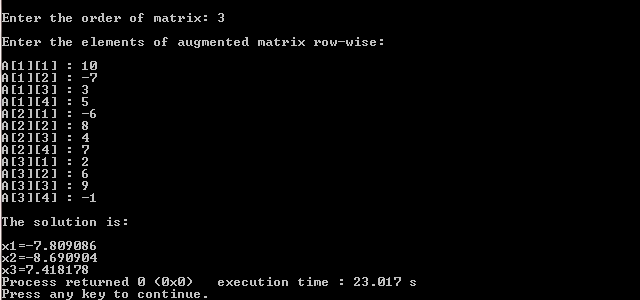
MATLAB Program

Named after Carl Friedrich Gauss, Gauss Elimination Method is a popular technique of linear algebra for solving system of linear equations. As the manipulation process of the method is based on various row operations of augmented matrix, it is also known as row reduction method. Gauss elimination method has various uses in finding rank of a matrix, calculation of determinant and inverse of invertible matrix.
In earlier tutorials, we discussed a C program and algorithm/flowchart for Gauss elimination method. Here, we’re going to write a program code for Gauss elimination method in MATLAB, go through its mathematical derivation, and compare the result obtained from MATLAB code with a numerical example.

Derivation of Gauss Elimination Method:

Consider the following system of linear equations:

A1x + B1y + C1z = D1 . . . . . . . ( 1 )
A2x + B2y + C2z = D2 . . . . . . . . ( 2 )
A3x + B3y + C3z = D3 . . . . . . . . . . ( 3)

In order to apply Gauss elimination method, we need to express the above three linear equations in matrix form as given below:

A =                                        B =

Arrange matrices A and B in the following form (augmented matrix):

Now, perform the following elementary row operations till it is reduced to echelon form by:

• Exchanging or swapping two rows
• Adding the certain multiple of one row to another row
• Multiplying a row by non-zero number

This procedure is repeated until the augmented matrix is reduced to following echelon form:

Thus, the solution of above system of linear equation is (a, b, c) i.e. x = a, y = b and z = c. The program for Gauss elimination method in MATLAB is based on this derivation.

Gauss Elimination Method in MATLAB:

function C = gauss_elimination(A,B) % defining the function 
A= [ 1 2; 4 5] % Inputting the value of coefficient matrix
B = [-1; 4] % % Inputting the value of coefficient matrix
    i = 1; % loop variable
    X = [ A B ]; 
    [ nX mX ] = size( X); % determining the size of matrix   
    while i <= nX % start of loop 
        if X(i,i) == 0 % checking if the diagonal elements are zero or not
            disp('Diagonal element zero') % displaying the result if there exists zero 
            return
        end
        X = elimination(X,i,i); % proceeding forward if diagonal elements are non-zero
        i = i +1;
    end    
    C = X(:,mX);
 
function X = elimination(X,i,j)
% Pivoting (i,j) element of matrix X and eliminating other column
 
% elements to zero
 
[ nX mX ] = size( X); 
a = X(i,j);
X(i,:) = X(i,:)/a;
for k =  1:nX % loop to find triangular form 
    if k == i
        continue
    end
    X(k,:) = X(k,:) - X(i,:)*X(k,j); % final result 
end

The above source code for Gauss elimination method in MATLAB can be used to solve any number of linear equations. The order of augmented matrix relies on the number of the linear equations to be solved by using this method. As the matrix element data are embedded within the source code, the user doesn’t need to give input to the program.

This source code is written to solve the following system of linear equation:

2x + y – z = 8
-3x – y + 2z = -11
-2x + y +2z = -3

Therefore, the value of A and B in the source code are fixed to be [ 2 1 -1; -3 -1 2; -2 1 2] and [8 ; -11 ; -3 ]
Instead of creating a separate MATLAB file to define the function and give input, a single file is designed to perform all the tasks. In order to solve other equation using this source code, the user has to change the values of augmented matrices A and B defined in the source code.
The sample output of the MATLAB program is given below:

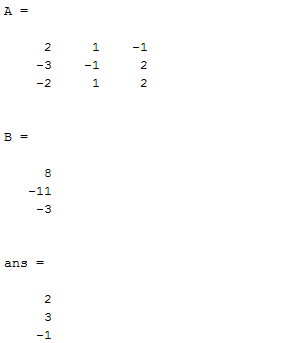
Gauss Elimination Method Numerical Example:

Now, let’s analyze numerically the above program code of Gauss elimination in MATLAB using the same system of linear equations. So, we are to solve the following system of linear equation by using Gauss elimination (row reduction) method:

2x + y – z = 8
-3x – y + 2z = -11
-2x + y +2z = -3

The given equations are:

2x + y – z = 8 . . . . . . . . . . . ( 1 )
-3x – y + 2z = -11 . . . . . . . . . ( 2 )
-2x + y +2z = -3 . . . . . . . . . . . ( 3 )

These can be expressed in the form of augmented matrix as:

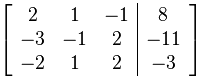
Performing Row Operations: L2 + 3/2 L1 –> L2 and L3 + L1 –>L3

The new augmented matrix is:

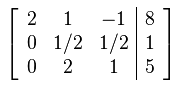
Performing row operation: L3 – 4L2 –>L3
The new augmented matrix is:

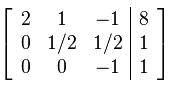
Row Operations: L2 + 1/3L3—> L2 and L1 – L3 –> L1
Augmented Matrix:

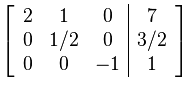
Row operations: 2L2 –> L2 and -L3–> L3
Augmented Matrix:

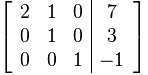
Row operations: L1 – L2 –> L1 and 1/2L1 –> L1
Augmented matrix:

Thus, x= 2 , y = 3 and z = -1. This is the required solution which is same as that obtained from Gauss elimination method’s MATLAB code.
If you have any questions regarding Gauss elimination method, its MATLAB program code, or its mathematical derivation, bring them up from the comments. You can find more Numerical methods tutorial using MATLAB here.

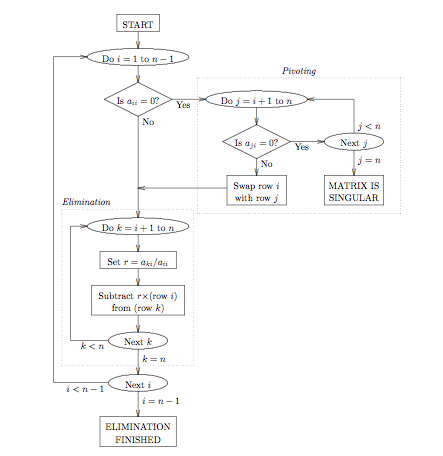
Algorithm and Flowchart

Gauss Elimination method can be adopted to find the solution of linear simultaneous equations arising in engineering problems. In the method, equations are solved by elimination procedure of the unknowns successively.
The method overall reduces the system of linear simultaneous equations to an upper triangular matrix. Then backward substitution is used to derive the unknowns. This is the key concept in writing an algorithm or program, or drawing a flowchart for Gauss Elimination.
Partial pivoting or complete pivoting can be adopted in Gauss Elimination method. So, this method is considered superior to the Gauss Jordan method.
In the Gauss Elimination method algorithm and flowchart given below, the elimination process is carried out until only one unknown remains in the last equation. It is straightforward to program, and partial pivoting can be used to control rounding errors.

Gauss Elimination Algorithm:

• Start
• Declare the variables and read the order of the matrix n.
• Take the coefficients of the linear equation as:
  Do for k=1 to n
  Do for j=1 to n+1
  Read a[k][j]
  End for j
  End for k
• Do for k=1 to n-1
  Do for i=k+1 to n
  Do for j=k+1 to n+1
  a[i][j] = a[i][j] – a[i][k] /a[k][k] * a[k][j]
  End for j
  End for i
  End for k
• Compute x[n] = a[n][n+1]/a[n][n]
• Do for k=n-1 to 1
  sum = 0
  Do for j=k+1 to n
  sum = sum + a[k][j] * x[j]
  End for j
  x[k] = 1/a[k][k] * (a[k][n+1] – sum)
  End for k
• Display the result x[k]
• Stop

Gauss Elimination Flowchart:

Here is a basic layout of Gauss Elimination flowchart which includes input, forward elimination, back substitution and output.

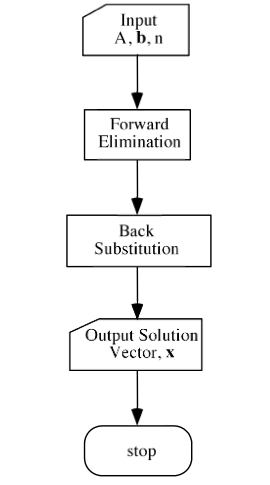
The one given below shows pivoting and elimination procedure.

Here is an attachment showing how the forward elimination and back substitution take place.

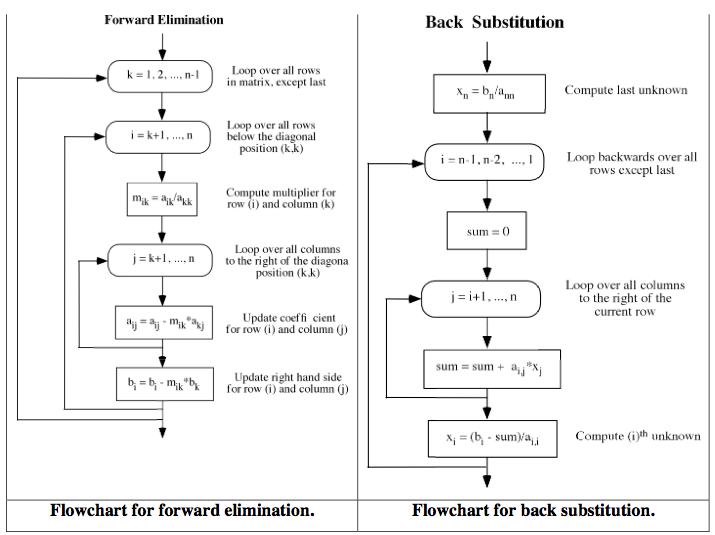
While solving linear simultaneous equations, analytical methods often fail when the problems are complicated. These algorithm and flowchart can be referred to write source code for Gauss Elimination Method in any high level programming language.