Muller’s Method

C Program

Muller’s method is an iterative generalization of the secant method for locating the complex roots of a function. It doesn’t require derivative of the function. The C program for Muller’s method requires three initial guesses and, mathematically, the approximation is done by a second degree parabola passing through these points. (Derivation)
The programming effort for Muller’s Method in C language is a bit tedious as it requires three initial approximations. However, the method converges quadratically for almost all the initial guesses. Overall, this method is more effective for locating complex roots – it can effectively generate complex roots of the function, even though the initial approximations or guesses are real.
Muller’s method converges slower than the Newton-Raphson method, but faster than the secant method. The convergence is linear and the overall approach used in the method is quadratic interpolation of the three guesses.
s Below is a short and simple source code in C program for Muller’s method to find the root of cos(x) – x*e^x .

• itr – a counter which keeps track of the no. of iterations performed
• maxmitr – maximum number of iterations to be performed

Source Code for Muller’s Method in C:

#include< stdio.h>
#include< math.h>
#define I 2
float f(float x)
{
    return cos(x) - x*exp(x);
}
main ()
{
    int i, itr, maxmitr;
    float x[4], li, di, mu, s, l, allerr;
    printf("\nEnter the three initial guesses:\n");
    for (i=I-2; i< 3; i++)
        scanf("%f", &x[i]);
    printf("Enter allowed error and maximum iterations:\n");
    scanf("%f %d", &allerr, &maxmitr);
    for (itr=1; itr<=maxmitr; itr++)
    {
        li = (x[I] - x[I-1]) / (x[I-1] - x[I-2]);
        di = (x[I] - x[I-2]) / (x[I-1] - x[I-2]);
        mu = f(x[I-2])*li*li - f(x[I-1])*di*di + f(x[I])*(di+li);
        s = sqrt ((mu*mu - 4*f(x[I])*di*li*(f(x[I-2])*li - f(x[I-1])*di + f(x[I]))));
        if (mu < 0)
            l = (2*f(x[I])*di)/(-mu+s);
        else
            l = (2*f(x[I])*di)/(-mu-s);
        x[I+1] = x[I] + l*(x[I] - x[I-1]);
        printf("At iteration no. %3d, x = %7.5f\n", itr, x[I+1]);
        if (fabs (x[I+1] - x[I]) < allerr)
        {
        printf("After %3d iterations, the required root is %6.4f\n", itr, x[I+1]);
        return 0;
        }
        for (i=I-2; i< 3; i++)
            x[i] = x[i+1];
    }
printf("The required solution does not converge or iterations are insufficient\n");
return 1;
}

Here, x is an array which holds the three initial guesses for the root and the new improved value obtained as I has been defined as 2 in the program. It is done in this way in this program because array subscripts always start from zero and are never negative. Further, the use of I facilitates more readable and understandable expressions.

Input/Output:

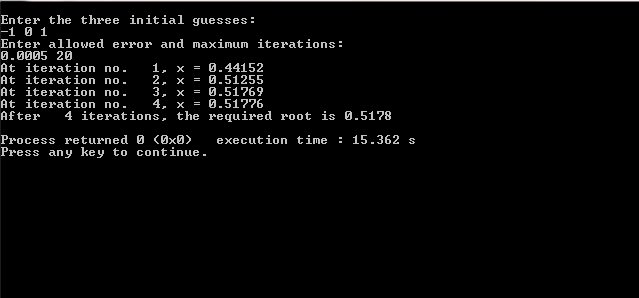
Muller’s Method was developed by David Muller in 1956. Considered not that useful to find the real roots of simple functions, it is a very effective method for finding complex roots. You can compare the above result obtained from the Muller’s method C program with that obtained from the Regula-Falsi Method.

Algorithm and Flowchart

Muller’s method is generalized a form of the secant method. This method was developed in 1956 by David Muller. It is generally used to locate complex roots of an equation. Unlike the Newton Raphson method, it doesn’t required the derivation of the function.
The convergence in Muller’s method is linear, faster than the secant method, but slower than the Newton Raphson method. The algorithm and flowchart for Muller’s method presented here require initial approximations in an array.
The algorithm or flowchart can be referred to write program for Muller’s method in any high level programming language. The approximation here is done by a parabola of second degree intersecting these points.
The effort in Muller’s method or its algorithm may be a bit tedious, but this can be made a bit simpler by taking only three initial guesses. The approach used here is quadratic interpolation of these guesses. However, the use of array can facilitate in more understandable and readable expressions.

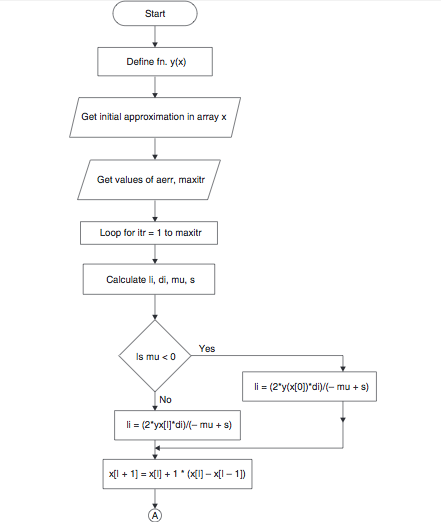
Muller’s Method Algorithm:

• Start
• Declare function f(x)
• Get initial approximation in array x
• Get values of aerr and maxitr
  *Here aerr is the absolute error
  Maxitr is the maximum number of iterations for the desired degree of accuracy*
• Loop for itr = 1 to maxitr
• Calculate li, di, mu and s
• If mu < 0,
  I = (2*y(x[0]*di)/(-mu + s)
• Else,
  I = (2*y(x[I]*di)/(-mu – s)
• x[I + 1] = x[I] + l*(x[I] – x[I – 1])
• Print itr and x[l]
• If fabs (x[l] – x[0]) < aerr,
  Print the required root as x[l]
• Else,
  Loop for i=0 to 2
  x[i] = x[i + l]
• End loop (i)
• End loop (itr)
• Print the solution does not converge
• Stop

Muller’s Method Flowchart:

Apart from the algorithm and flowchart presented here, Muller’s method itself is not considered much effective for locating the real roots of a function. As, the method converges quadratically for the initial approximations, it is more useful when it comes to locating the complex roots of a function. So, Muller’s method can effectively produce complex roots, even though the initial guesses are real.