Theoretical Paper
- Computer Organization
- Data Structure
- Digital Electronics
- Object Oriented Programming
- Discrete Mathematics
- Graph Theory
- Operating Systems
- Software Engineering
- Computer Graphics
- Database Management System
- Operation Research
- Computer Networking
- Image Processing
- Internet Technologies
- Micro Processor
- E-Commerce & ERP
- Dart Programming
- Flutter Tutorial
- Numerical Methods Tutorials
Practical Paper
Industrial Training
Newton Raphson Method
C Program
Newton-Raphson method, also known as the Newton’s Method, is the simplest and fastest approach to find the root of a function. It is an open bracket method and requires only one initial guess. The C program for Newton Raphson method presented here is a programming approach which can be used to find the real roots of not only a nonlinear function, but also those of algebraic and transcendental equations.
Newton’s method is often used to improve the result or value of the root obtained from other methods. This method is more useful when the first derivative of f(x) is a large value.
The programming effort for Newton Raphson Method in C language is relatively simple and fast. The convergence is the fastest of all the root finding methods discussed in Numerical Methods Tutorial section – the bisection method, the secant method and the regula-falsi method.
Features of Newton Raphson Method:
- Type – open bracket
- No. of initial guesses – 1
- Convergence – quadratic
- Rate of convergence – faster
- Accuracy – good
- Programming effort – easy
- Approach – Taylor’s series
Below is a very short and simple source code in C program for Newton’s method to find the root of x*log10(x) – 1.2.
Variables:
- itr – a counter which keeps track of the no. of iterations performed
- maxmitr – maximum number of iterations to be performed
- df(x) – the derivative of f(x) with respect to x
- x0 – the value of root at nth iteration
- x1 – the value of root at (n+1)th iteration
- allerr – allowed error
f(x) = x*log10(x) – 1.2
Source Code for Newton Raphson Method in C:
#include#include float f(float x) { return x*log10(x) - 1.2; } float df (float x) { return log10(x) + 0.43429; } void main() { int itr, maxmitr; float h, x0, x1, allerr; printf("\nEnter x0, allowed error and maximum iterations\n"); scanf("%f %f %d", &x0, &allerr, &maxmitr); for (itr=1; itr<=maxmitr; itr++) { h=f(x0)/df(x0); x1=x0-h; printf(" At Iteration no. %3d, x = %9.6f\n", itr, x1); if (fabs(h) < allerr) { printf("After %3d iterations, root = %8.6f\n", itr, x1); return 0; } x0=x1; } printf(" The required solution does not converge or iterations are insufficient\n"); return 1; }
Input/Output:
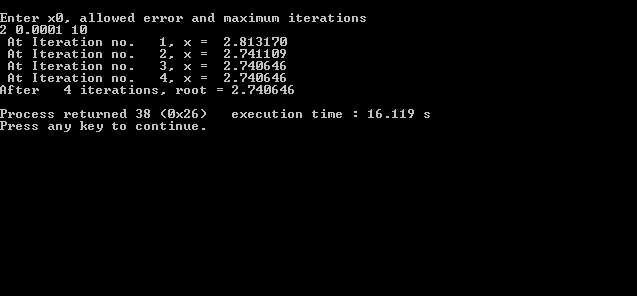
Limitations of Newton-Raphson Method:
- Finding the f'(x) i.e. the first derivative of f(x) can be difficult if f(x) is complicated.
- When f'(xn) tends to zero i.e. the first derivative of f(xn) tends to zero, Newton-Raphson method gives no solution.
- Near local maxima or local minima, there is infinite oscillation resulting in slow convergence.
- In Newton’s method C program, if the initial guess is far from the desired root, then the method may converge to some other roots.
- If root jumping occurs, the intended solution is not obtained.
MATLAB Program
Newton-Raphson method, named after Isaac Newton and Joseph Raphsonis a popular iterative method to find the root of a polynomial equation. It is also known as Newton’s method, and is considered as limiting case of secant method.
Based on the first few terms of Taylor’s series, Newton-Raphson method is more used when the first derivation of the given function/equation is a large value. It is often used to improve the value of the root obtained using other rooting finding methods in Numerical Methods.
We have already discussed C program and algorithm/flowchart for Newton’s method in earlier tutorials. Here, we are going to go through a sample program code for Newton Raphson method in MATLAB, along with a numerical example and theoretical background.
Derivation of Newton-Raphson Method:
The theoretical and mathematical background behind Newton-Raphson method and its MATLAB program (or program in any programming language) is approximation of the given function by tangent line with the help of derivative, after choosing a guess value of root which is reasonably close to the actual root.
The x- intercept of the tangent is calculated by using elementary algebra, and this calculated x-intercept is typically better approximation to the root of the function. This procedure is repeated till the root of desired accuracy is found.
Lets now go through a short mathematical background of Newton’s method. For this, consider a real value function f(x) as shown in the figure below:
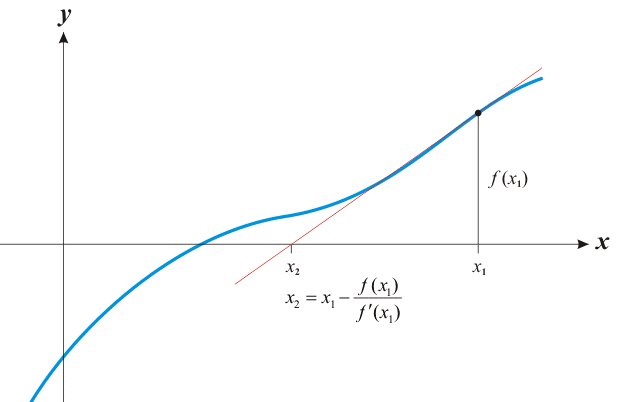
Consider x1 to be the initial guess root of the function f(x) which is essentially a differential function. Now, to derive better approximation, a tangent line is drawn as shown in the figure. The equation of this tangent line is given by:
y = f’(x1) (x- x1) + f(x1)
where, f’(x) is the derivative of function f(x).
As shown in the figure, f(x2) = 0 i.e. at x = x2, y=0
Therefore, 0 = f’(x1) (x2– x1) + f(x1)
Solving, x2 = x1 – f(x1) / f’(x1)
Repeating the above process for xn and xn+1 terms of the iteration process, we get the general iteration formula for Newton-Raphson Method as:
xn+1 = xn – f(xn)/f’(xn)
This formula is used in the program code for Newton Raphson method in MATLAB to find new guess roots.
Steps to find root using Newton’s Method:
- Check if the given function is differentiable or not. If the function is not differentiable, Newton’s method cannot be applied.
- Find the first derivative f’(x) of the given function f(x).
- Take an initial guess root of the function, say x1.
- Use Newton’s iteration formula to get new better approximate of the root, say x2 x2 = x1 – f(x1)/f’(x1)
- Repeat the process for x3, x4… till the actual root of the function is obtained, fulfilling the tolerance of error.
Newton Raphson Method in MATLAB:
% Program Code of Newton-Raphson Method in MATLAB
a=input('Enter the function in the form of variable x:','s');
x(1)=input('Enter Initial Guess:');
error=input('Enter allowed Error:');
f=inline(a)
dif=diff(sym(a));
d=inline(dif);
for i=1:100
x(i+1)=x(i)-((f(x(i))/d(x(i))));
err(i)=abs((x(i+1)-x(i))/x(i));
if err(i)< error
break
end
end
root=x(i)
In this code for Newton’s method in Matlab, any polynomial function can be given as input. Initially in the program, the input function has been defined and is assigned to a variable ‘a’.
After getting the initial guess value of the root and allowed error, the program, following basic MATLAB syntax, finds out root undergoing iteration procedure as explained in the theory above. Here’s a sample output of this code:

Newton-Raphson Method Example:
Now, lets analyze the above program of Newton-Raphson method in Matlab, taking the same function used in the above program and solving it numerically. The function is to be corrected to 9 decimal places.
Solution:
Given function: x3−x−1 = 0, is differentiable.
The first derivative of f(x) is f’(x) = 3x2 – 1
Lets determine the guess value.
f(1) = 1 -1 -1 = -1 and f(2) = 8 – 2 -1 = 5
Therefore, the root lies in the interval [1, 2]. So, assume x1= 1.5 as the initial guess root of the function f(x) = x3−x−1.
Now,
f(1.5) = 1.53 – 1.5 – 1 = 0.875
f’(1.5) = 3 * 1.52– 1 = 5.750
Using Newton’s iteration formula:
x2 = x1 – f(x1)/f’(x1) = 1.5 – 0.875/5.750 = 1.34782600
The iteration for x3, x4, …. is done similarly.
The table below shows the whole iteration procedure for the given function in the program code for Newton Raphson in MATLAB and this numerical example.
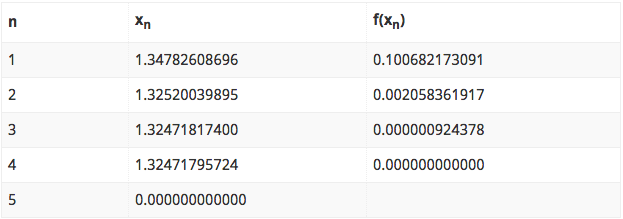
Therefore, x = 1.324717957 is the desired root of the given function, corrected to 9 decimal places. The MATLAB program gives the result x = 1.3252 only, but this value can be improved by improving the value of allowable error entered.
Algorithm and Flowchart
Newton Raphson method, also called the Newton’s method, is the fastest and simplest approach of all methods to find the real root of a nonlinear function. It is an open bracket approach, requiring only one initial guess. This method is quite often used to improve the results obtained from other iterative approaches.
The convergence is fastest of all the root-finding methods we have discussed in Code with C. The algorithm and flowchart for Newton Raphson method given below is suitable for not only find the roots of a nonlinear equation, but the roots of algebraic and transcendental equations as well.
The overall approach of Newton’s method is more useful in case of large values the first derivative of f(X) i.e f'(X). The iterative formula for Newton Raphson method is:
[highlight color=”yellow”]Xn+1 = Xn – f(Xn)/f'(Xn)[/highlight]
Features of Newton’s Method:
- Type – open bracket
- No. of initial guesses – 1
- Convergence – quadratic
- Rate of convergence – faster
- Accuracy – good
- Programming effort – easy
- Approach – Taylor’s series
Newton Raphson Method Algorithm:
- Start
- Read x, e, n, d
*x is the initial guess
e is the absolute error i.e the desired degree of accuracy
n is for operating loop
d is for checking slope* - Do for i =1 to n in step of 2
- f = f(x)
- f1 = f'(x)
- If ( [f1] < d), then display too small slope and goto 11.
*[ ] is used as modulus sign* - x1 = x – f/f1
- If ( [(x1 – x)/x1] < e ), the display the root as x1 and goto 11.
*[ ] is used as modulus sign* - x = x1 and end loop
- Display method does not converge due to oscillation.
- Stop
Newton Raphson Method Flowchart:
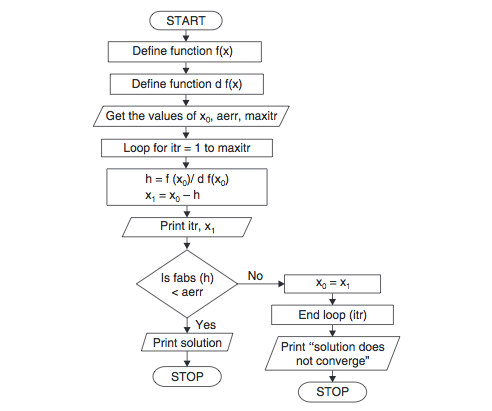
These algorithm and flowchart can be used to write source code for Newton’s method in any high level programming language.
Although the Newton Raphson method is considered fast, there are some limitations. These are listed below:
- Finding the f’(x) i.e. the first derivative of f(x) can be difficult in cases where f(x) is complicated.
- When f’(xn) i.e. the first derivative of f(xn) tends to zero, Newton Raphson gives no solution.
- Infinite oscillation resulting in slow convergence near local maxima or minima.
- If the initial guess is far from the desired root, then the method may converge to some other roots. So, Newton Raphson method is quite sensitive to the starting value.
- The method cannot be applied suitably when the graph of f(x) is nearly horizontal while crossing the x-axis.
- If root jumping occurs, the intended solution is not obtained.

