Lu Factorization

C Program

For this C program for LU factorization, consider a general linear system AX = b, such that the given matrix [A] is factorized into the product of two upper and lower triangular matrices. The solution of linear simultaneous equations sought this way is called LU factorization method. This method is also known as the Triangular method or the LU Decomposition method.
So, the basic principle here is – “A square matrix [A] can be written as the product of a lower triangular matrix [L] and an upper triangular matrix [U], one of them being unit triangular, if all the principal minors of [A] are non-singular . Now, see how the matrix undergoes decomposition in the program for LU Factorization in C language.

[A] = [L][U]

where, L is the lower triangular matrix and U is the upper triangular matrix. The elements of these three matrices row-wise are:

[A] = {a11, a12, a13, a21, a22, a23, a31, a32, a33}
[L] = {1, 0, 0, l21, 1, 0, l31, l32, 1}
[U] = {u11, u12, u13, 0, u22, u23, 0, 0, u33}

The representation obtained upon putting these elements in the 1st expression aforementioned is termed as LU factorization. It is simply a product of a lower and an upper triangular matrix decomposed from the parent matrix A. The diagonal non-zero entry of [L] is the ith pivot during factorization. The elements of matrix A can be obtained by multiplying [L] and [U].

This factorization method is preferred over the Gauss Elimination method in computers and programming languages like C. It facilitates obtaining products in double length. This C program below illustrates the application of LU Factorization method based on the things mentioned above.

Source Code for LU Factorization in C:

#include< stdio.h>
#include< conio.h>
void main()
{
    float A[20][20]= {0},L[20][20]= {0}, U[20][20];
    float B[20]= {0}, X[20]= {0},Y[20]= {0};
    int i,j,k,n;
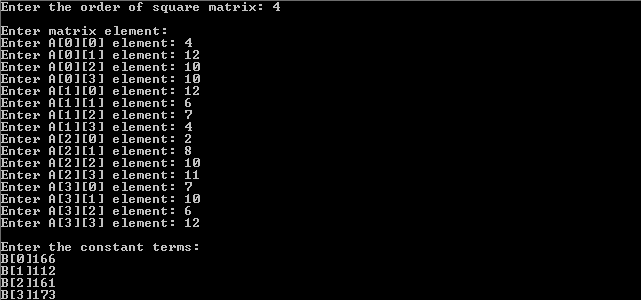
    printf("Enter the order of square matrix: ");
    scanf("%d",&n);
    printf("\nEnter matrix element:\n");
    for(i=0; i< n; i++)
    {
        for(j=0; j< n; j++)
        {
            printf("Enter A[%d][%d] element: ", i,j);
            scanf("%f",&A[i][j]);
        }
    }
    printf("\nEnter the constant terms: \n");
    for(i=0; i< n; i++)
    {
        printf("B[%d]",i);
        scanf("%f",&B[i]);
    }
    for(j=0; j< n; j++)
    {
        for(i=0; i< n; i++)
        {
            if(i<=j)
            {
                U[i][j]=A[i][j];
                for(k=0; k< i-1; k++)
                    U[i][j]-=L[i][k]*U[k][j];
                if(i==j)
                    L[i][j]=1;
                else
                    L[i][j]=0;
            }
            else
            {
                L[i][j]=A[i][j];
                for(k=0; k<=j-1; k++)
                    L[i][j]-=L[i][k]*U[k][j];
                L[i][j]/=U[j][j];
                U[i][j]=0;
            }
        }
    }
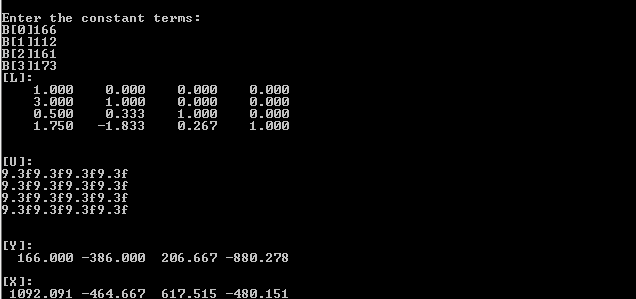
    printf("[L]: \n");
    for(i=0; i< n; i++)
    {
        for(j=0; j< n; j++)
            printf("%9.3f",L[i][j]);
        printf("\n");
    }
    printf("\n\n[U]: \n");
    for(i=0; i< n; i++)
    {
        for(j=0; j< n; j++)
            printf("%9.3f",U[i][j]);
        printf("\n");
    }
    for(i=0; i< n; i++)
    {
        Y[i]=B[i];
        for(j=0; j< i; j++)
        {
            Y[i]-=L[i][j]*Y[j];
        }
    }
    printf("\n\n[Y]: \n");
    for(i=0; i< n; i++)
    {
        printf("%9.3f",Y[i]);
    }
    for(i=n-1; i>=0; i--)
    {
        X[i]= Y[i];
        for(j=i+1; j< n; j++)
        {
            X[i]-=U[i][j]*X[j];
        }
        X[i]/=U[i][i];
    }
    printf("\n\n[X]: \n");
    for(i=0; i< n; i++)
    {
        printf("%9.3f",X[i]);
    }
    getch();
}

Input/Output:

Algorithm and Flowchart

LU decomposition, also known as LU factorization, is one of the common methods adopted to find the solution of linear simultaneous equations in numerical analysis and other engineering problems. In this post, I have included simple algorithm and flowchart for LU factorization method. Here’s a brief introduction to the method, and algorithm samples for Doolittle’s and Crout’s LU decomposition.
The basic principle used to write the LU decomposition algorithm and flowchart is – ““A square matrix [A] can be written as the product of a lower triangular matrix [L] and an upper triangular matrix [U], one of them being unit triangular, if all the principal minors of [A] are non-singular.”
So, for a linear system AX = b, the given matrix [A] can be decomposed into the product two lower and upper triangular matrices.
Here, I have presented a simple flowchart for the method. For the algorithm part, you can find images for Doolittle’s LU algorithm, Crout’s LU algorithm and a short algorithm for LU decomposition method itself.

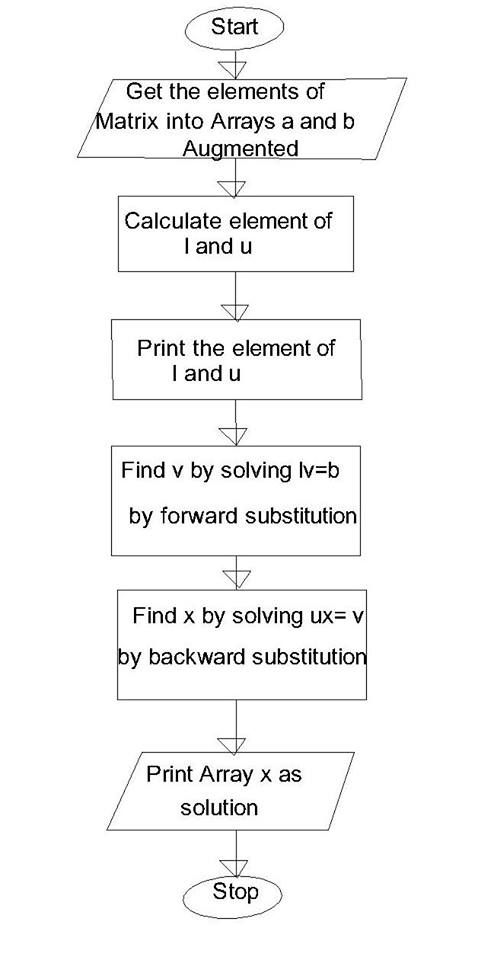
LU Factorization Algorithm:

• Start
• Read the elements of augmented matrix into arrays a and b
• Calculate elements of L and U
• Print elements of L and U
• Find V by solving LV = B by forward substitution
• Find X by solving UX = V by backward substitution
• Print Array X as the solution
• Stop

The principle difference between Doolittle’s and Crout’s LU decomposition method is the calculation sequence these methods follow. Both the methods exhibit similarity in terms of inner product accumulation.
In Doolittle’s method, calculations are sequenced to compute one row of L followed by the corresponding row of U until A is exhausted. Below is the computational sequence and algorithm for Doolittle’s LU decomposition.

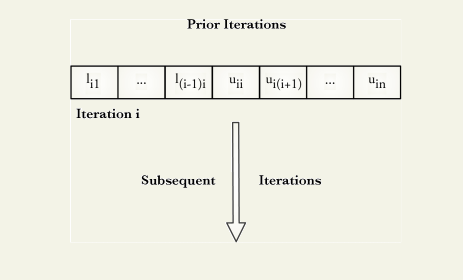
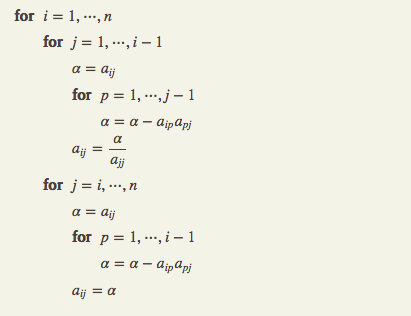
Whereas in Crout’s method, calculations are sequenced to compute one column of L followed by the corresponding row of U until A is exhausted. Below is the computational sequence and algorithm for Crout’s LU decomposition.

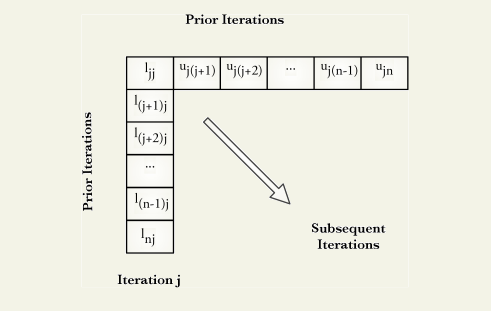
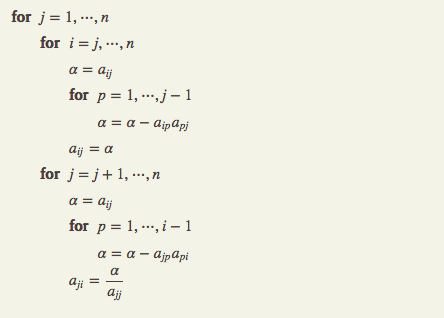
LU Decomposition Flowchart: