Fixed Point Iteration Method

C Program

Fixed point iteration method is commonly known as the iteration method. It is one of the most common methods used to find the real roots of a function. The C program for fixed point iteration method is more particularly useful for locating the real roots of an equation given in the form of an infinite series. So, this method can be used for finding the solution of arithmetic series, geometric series, Taylor’s series and other forms of infinite series.
This method is linearly convergent with somewhat slower rate of convergence, similar to the bisection method. It is based on modification approach to find the fixed point. It is commonly referred to as simple enclosure method or open bracket method.
Like other methods to find the root of a function, the programming effort for Iteration Method in C is easy, short and simple. Just like the Newton-Raphson method, it requires only one initial guess, and the equation is solved by the assumed approximation.
Iterations and modifications are successively continued with the updated approximations of the guess. Iterative method gives good accuracy overall just like the other methods.

• Type – open bracket
• No. of initial guesses – 1
• Convergence – linear
• Rate of convergence – fast
• Accuracy – good
• Programming effort – easy
• Approach – modification

Below is a source code in C program for iteration method to find the root of (cosx+2)/3. The desired degree of accuracy in the program can be achieved by continuing the iteration i.e. by increasing the maximum number of iterations. f(x) = (cos(x) +2)/3

Source Code for Iteration Method in C:

#include< stdio.h>
#include< math.h>
float raj(float);
main()
{
    float a[100],b[100],c=100.0;
    int i=1,j=0;
    b[0]=(cos(0)-3*0+1);
    printf("\nEnter initial guess:\n");
    scanf("%f",&a[0]);
    printf("\n\n The values of iterations are:\n\n ");
    while(c>0.00001)
    {
        a[j+1]=raj(a[j]);
        c=a[j+1]-a[j];
        c=fabs(c);
        printf("%d\t%f\n",j,a[j]);
        j++;
 
    }
    printf("\n The root of the given function is %f",a[j]);
}
float raj(float x)
{
    float y;
    y=(cos(x)+2)/3;
    return y;
}

Input/Output:

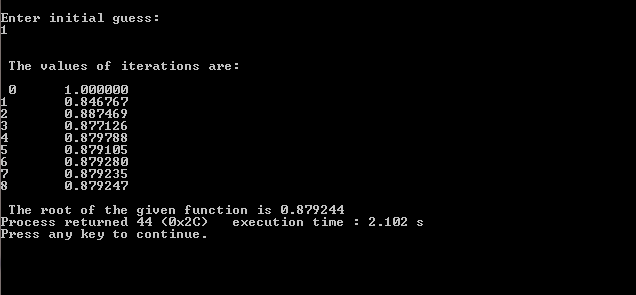
The fixed point iteration method is found extensively useful in many mathematical formulations and theorems. It is often used to find solutions and approximations to successive guess strategies used in dynamic engineering problems. Some of the popular methods utilizing this method are Newton’s method, Halley’s method, Runge-Kutta methods and the Picard–Lindelöf theorem.
Any questions or queries regarding fixed point iteration method or its C language source code presented here can be discussed and brought up to us from the comments section.

Algorithm and Flowchart

Iteration method, also known as the fixed point iteration method, is one of the most popular approaches to find the real roots of a nonlinear function. It requires just one initial guess and has a fast rate of convergence which is linear.
These algorithm and flowchart presented here and the iteration method itself are used to determine the real roots of functions in the form of an infinite series such as the geometric series, arithmetic series, Taylor’s series, and others.
Similar to the Newton-Raphson method, both the algorithm and flowchart in case of iteration method require one initial guess. And, just like the bisection method, this method has slow and linear convergence.
Iterative method is also referred to as an open bracket method or a simple enclosure method. It is based on modification approach to find the root of the function. Overall, it gives good accuracy just like the other methods.
A function f(x) = 0 is solved by the assumed initial guess. The fixed point iteration method algorithm/flowchart work in such as way that modifications alongside iteration are progressively continued with the newer and fresher approximations of the initial approximation.

Features of Iteration Method:

• No. of initial guesses – 1
• Type – open bracket
• Rate of convergence – fast
• Convergence – linear
• Approach – modification
• Accuracy – good
• Programming effort – easy

Iteration Method Algorithm:

Iteration Method Flowchart:

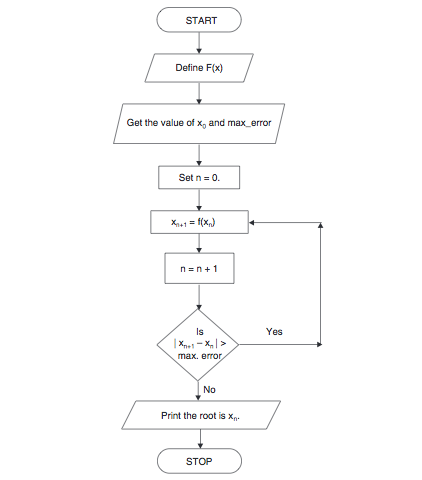
This fixed point iteration method algorithm and flowchart comes to be useful in many mathematical formulations and theorems. Often, approximations and solutions to iterative guess strategies utilized in dynamic engineering problems are sought using this method.
Some of the well-known methods or derivations utilizing this method are Picard–Lindelöf theorem. Newton’s method, Runge-Kutta methods and Halley’s method.