Power Method

C Program

Power method is used to find the dominant eigen value and the corresponding eigen vector. Eigen value problems generally arise in dynamics problems and structural stability analysis. Power method is generally used to calculate these eigen value and corresponding eigen vector of the given matrix.
The C program for power method is just a programming illustration of power method as one of the most well suited iterative approach for machine computations. With this, the numerically greatest eigen value and the subsequent eigen vector can be computed to analyze different engineering problems.
Before going into the program for Power Method in C language, let’s look at a simple mathematical formulation of eigen values and eigen vector. For this, consider a matrix A. We have to find the column vector X and the constant L (L=lamda) such that:

[A]{X} = L{X}

Now, consider these three set of equations:

a11x1 + a12x2 + a13x3 = Lx1
a12x1 + a22x2 + a23x3 = Lx2
a31x1 + a32x2 + a33x3 = Lx3

These equations can be written as:

(a11-L)x1 +a12x2 +a13x3 = 0
a21x1 +(a22-L)x2 +a23x3 = 0
a31x1 +a32x2 + (a33-L)x3 = 0

Now the determinant of the 3*3 matrix formed of the coefficients of x1, x2 and x3 terms gives three roots, namely L1, L2 and L3 (read L as lamda). These values are called characteristic or eigen values. For each of these values, we get a set of column vector with elements x1, x2 and x3. This vector is the required eigen vector.
The Power method C program given below utilizes continuous approximation of L (lamda) to the eigen value and X to the eigen vector. For this method, the matrix should be symmetric or positive definitive i.e. aij = aji.

Source Code for Power Method in C:

#include< stdio.h>
#include< conio.h>
#include< math.h>
void main()
{
 
    int i,j,n;
    float A[40][40],x[40],z[40],e[40],zmax,emax;
    printf("\nEnter the order of matrix:");
    scanf("%d",&n);
    printf("\nEnter matrix elements row-wise\n");
    for(i=1; i<=n; i++)
    {
        for(j=1; j<=n; j++)
        {
            printf("A[%d][%d]=", i,j);
            scanf("%f",&A[i][j]);
        }
    }
    printf("\nEnter the column vector\n");
    for(i=1; i<=n; i++)
    {
        printf("X[%d]=",i);
        scanf("%f",&x[i]);
    }
    do
    {
        for(i=1; i<=n; i++)
        {
            z[i]=0;
            for(j=1; j<=n; j++)
            {
                z[i]=z[i]+A[i][j]*x[j];
            }
        }
        zmax=fabs(z[1]);
        for(i=2; i<=n; i++)
        {
            if((fabs(z[i]))>zmax)
                zmax=fabs(z[i]);
        }
        for(i=1; i<=n; i++)
        {
            z[i]=z[i]/zmax;
        }
        for(i=1; i<=n; i++)
        {
            e[i]=0;
            e[i]=fabs((fabs(z[i]))-(fabs(x[i])));
        }
        emax=e[1];
        for(i=2; i<=n; i++)
        {
            if(e[i]>emax)
                emax=e[i];
        }
        for(i=1; i<=n; i++)
        {
            x[i]=z[i];
        }
    }
    while(emax>0.001);
    printf("\n The required eigen value is %f",zmax);
    printf("\n\nThe required eigen vector is :\n");
    for(i=1; i<=n; i++)
    {
        printf("%f\t",z[i]);
    }
    getch();
}

Input/Output:

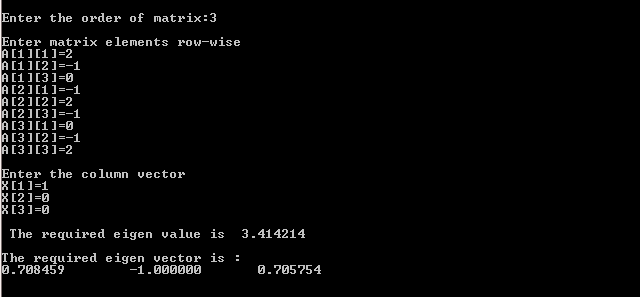
MATLAB Program

Power Method, used in mathematics and numerical methods, is an iteration method to compute the dominant eigenvalue and eigenvector of a matrix. It is a simple algorithm which does not compute matrix decomposition, and hence it can be used in cases of large sparse matrices. Power method gives the largest eigenvalue and it converges slowly.
In earlier tutorials, we discussed algorithm/flowchart and C program for power method. Here, we are going to write a program source code for Power method in MATLAB and go through its theoretical background along with a numerical example.

Theoretical Background of Power Method:

In linear algebra, eigenvalue of a square matrix is defined as a vector which points invariant direction under the associated linear transformation. If λ be the eigenvalue of a square matrix A, it can be mathematically depicted as:

Av = λv

where, ‘v’ is a vector (called eigenvector) which is non-zero. This vector ‘v’ is said to be normalized if its coordinate of largest magnitude is unity.

Consider a matrix A of order mxn which has n distinct eigenvalues λ1, λ2, λ3,… λn. The descending order of these eigenvalues can be given as:

|λ1| > |λ2| > |λ3| …… > |λn|

Choose an appropriate value of x0 . Now, the sequence can be given as:

{ xk = (x1(k), x2(k), x3(k), ………. xn(k))T}
The sequence of {Ck} is generated by:
Yn = AXk and Xk+1 = 1/(Ck+1) * Yk
where, Ck+1 = Xj(k) and Xj (k) = max{|xi(k)|
These values will converge to the dominant eigenvalue λ1 and eigenvector v1.

Power Method uses continuous guesses of X to the eigenvector and λ to the eigenvalue. In both manual calculation and programming approach (MATLAB code) of Power method, the matrix must be symmetric i.e. aij = aji.
Now, again consider a matrix A, whose eigenvector X and eigenvalue λ are to be found out, such that:

[A]{X} = λ{X}

Say, we’re given these three set of equations:

a11x1 + a12x2 + a13x3 = λx1
a12x1 + a22x2 + a23x3 = λx2
a31x1 + a32x2 + a33x3 = λx3

These equations can be re-written as:

(a11-λ)x1 +a12x2 +a13x3 = 0
a21x1 +(a22-λ)x2 +a23x3 = 0
a31x1 +a32x2 + (a33-λ)x3 = 0

Hence, the determinant of the 3*3 matrix thus formed out of the coefficients of ‘x’ terms gives three roots: λ1, λ2 and λ3. These roots are the required eigenvalues or characteristic values.

And, for each of these values, we obtain a set of column vector with elements x1, x2 and x3. This vector is the required eigenvector. This technique is utilized in the below program for Power method in MATLAB.

Google uses power iteration method to calculate the PageRank of webpages in their search engine! Also, the recommendations like “who to follow” in Twitter are based on this method!

Power Method in MATLAB:

function [ v d] = power_method( A )
% for finding the largest eigen value by power method
 
 
disp ( ' Enter the matrix whose eigen value is to be found')
 
% Calling matrix A
 
A = input ( ' Enter matrix A :   \n')
% check for matrix A
 
% it should be a square matrix
 
[na , ma ] = size (A);
if na ~= ma
    disp('ERROR:Matrix A should be a square matrix')
    return
end
 
% initial guess for X..?
 
% default guess is [ 1 1 .... 1]'
 
disp('Suppose X is an eigen vector corresponding to largest eigen value of matrix A')
r = input ( 'Any guess for initial value of X? (y/n):   ','s');
switch r 
    case 'y'
        % asking for initial guess
    X0 = input('Please enter initial guess for X :\n')
        % check for initial guess
    [nx, mx] = size(X0);
    if nx ~= na || mx ~= 1
        disp( 'ERROR: please check your input')
        return
    end
    otherwise
    X0 = ones(na,1);
end
 
%allowed error in final answer
 
t = input ( 'Enter the error allowed in final answer:  ');
tol = t*ones(na,1);
% initialing k and X
 
k= 1;
X( : , 1 ) = X0;
 %initial error assumption
err= 1000000000*rand(na,1);
% loop starts
 
while sum(abs(err) >= tol) ~= 0
    X( : ,k+ 1 ) = A*X( : ,k); %POWER METHOD formula
    % normalizing the obtained vector 
    [ v i ] = max(abs(A*X( : ,k+ 1 )));
    E = X( : ,k+ 1 );
    e = E( i,1);
    X(:,k+1) = X(:,k+1)/e;
    err = X( :,k+1) - X( :, k);% finding error
    k = k + 1;  
end
 
%display of final result
 
fprintf (' The largest eigen value obtained after %d itarations is  %7.7f  \n', k, e)
disp('and the corresponding eigen vector is ')
X( : ,k)

The above code for power method in MATLAB is used to calculate the eigenvalue and eigenvector of a square matrix of any order by using iteration principle of power method. In this program, the matrix whose eigenvalue is to be determined is the input and its corresponding eigenvalue and eigenvector are the output.
As the program is executed, it asks for the value of matrix whose eigenvalue and eigenvector are to be found out. After that, the input matrix is checked whether it is square or not. If the matrix is not a square matrix, an error message is displayed. Further, the matrix should be symmetric or positive definitive.
Then, an initial guess value is to be given to the code, and based on that value and following the theory explained above, the program calculates eigenvalue and eigenvector of the entered matrix. Here’s a sample output of the program:

Power Method Numerical Example:

Let’s now analyze numerically the above program for power method in MATLAB with this example. We have to find out the dominant eigenvalue of the following matrix using Power method:

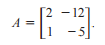
First, assume an initial iteration vector as:

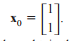
Now, the following approximation can be obtained:

Thus, the eigenvalue of the given matrix is 190 and the eigenvector is [3 1].

If you have any questions regarding Power method or its MATLAB code, bring them up the comments section. You can find more Numerical Methods tutorial using MATLAB here.

Algorithm and Flowchart

Power method is used to find the largest Eigen value and the corresponding Eigen vector for a given system of linear simultaneous equations. In this post, I have included simple algorithm and flowchart for Power method to calculate eigen value and eigen vector. Eigen value problems are generally encountered in dynamics problems and structural stability analysis.
To students, Eigen value problems may seem to be theoretical and raw. But in reality, these sort of problems arise in numerous engineering and scientific analysis. Eigen values are required for analyzing the frequencies associated with various phenomena such as:

• vibrations of beams
• systematic vibrations of of an annular membrane
• the vibrations of a system of springs and masses
• the oscillations of a triple pendulum
• the torsional oscillations of a multi-cylinder engine
• the torsional oscillations of a uniform cantilever structure, and more.

For the Power Method algorithm and flowchart, we will consider a given matrix A for which we have to find the column vector X and a constant L (read as Lamda) such that:

[A] [X] = L [X] which gives
{ [A] – L [I] } [X] = [0]

Now, for a system with 3 linear algebraic equations, we get
– a set of {X1, X2, X3} column vector for L1
– a set of {X1, X2, X3} column vector for L2
– a set of {X1, X2, X3} column vector for L3

Power Method Algorithm:

• Start
• Define matrix X
• Calculate Y = AX
• Find the largest element in magnitude of matrix Y and assign it to K.
• Calculate fresh value X = (1/K) * Y
• If [Kn – K(n-1)] > delta, goto step 3.
• Stop

Power Method Flowchart:

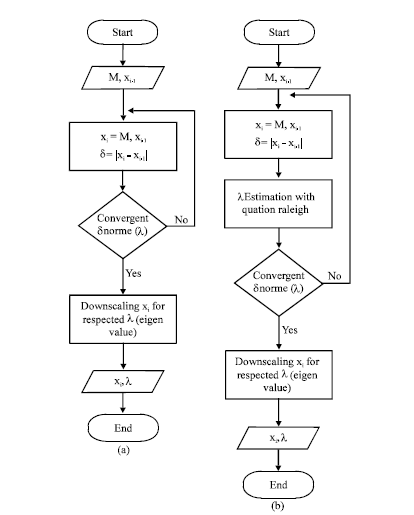
The procedure for Power method and these algorithm and flowchart to calculate the Eigen value and the corresponding Eigen vector is based on the method of “Characteristic polynomial”. For finding the dominant Eigen value of a given matrix, the iterative procedure implemented is known as “Rayleigh’s power method”.

With the power method algorithm and flowchart presented here, you can write source code for Power method in any high level programming language. The algorithm and flowchart are not exactly similarly presented with respect to one another. But, being based on iterative method, they are quite convenient to implement, and the method overall is well-suited for machine computations as well.