Gauss Jordan Method

C Program

The Gauss-Jordan method is used to analyze different systems of linear simultaneous equations that arise in engineering and science. This method finds its application in examining a network under sinusoidal steady state, output of a chemical plant, electronic circuits consisting invariant elements, and more.
The C program for Gauss-Jordan method is focused on reducing the system of equations to a diagonal matrix form by row operations such that the solution is obtained directly. Further, it reduces the time and effort invested in back-substitution for finding the unknowns, but requires a little more calculation. (see example)
The Gauss-Jordan method is simply a modification of the Gauss elimination method. The eliminations of the unknowns is performed not only in the equations below, but in those above as well. That is to say – unlike the elimination method, where the unknowns are eliminated from pivotal equation only, this method eliminates the unknown from all the equations.
The program of Gauss-Jordan Method in C presented here diagonalizes the given matrix by simple row operations. The additional calculations can be a bit tedious, but this method, overall, can be effectively used for small systems of linear simultaneous equations.
In the Gauss-Jordan C program, the given matrix is diagonalized using the following step-wise procedure.

• The element in the first column and the first row is reduced 1, and then the remaining elements in the first column are made 0 (zero).
• The element in the second column and the second row is made 1, and then the other elements in the second column are reduced to 0 (zero).
• Similarly, steps 1 and 2 are repeated for the next 3rd, 4th and following columns and rows.
• The overall diagonalization procedure is done in a sequential manner, performing only row operations.

Source Code for Gauss-Jordan Method in C:

#include< stdio.h>
int main()
{
    int i,j,k,n;
    float A[20][20],c,x[10];
    printf("\nEnter the size of matrix: ");
    scanf("%d",&n);
    printf("\nEnter the elements of augmented matrix row-wise:\n");
    for(i=1; i<=n; i++)
    {
        for(j=1; j<=(n+1); j++)
        {
            printf(" A[%d][%d]:", i,j);
            scanf("%f",&A[i][j]);
        }
    }
    /* Now finding the elements of diagonal matrix */
    for(j=1; j<=n; j++)
    {
        for(i=1; i<=n; i++)
        {
            if(i!=j)
            {
                c=A[i][j]/A[j][j];
                for(k=1; k<=n+1; k++)
                {
                    A[i][k]=A[i][k]-c*A[j][k];
                }
            }
        }
    }
    printf("\nThe solution is:\n");
    for(i=1; i<=n; i++)
    {
        x[i]=A[i][n+1]/A[i][i];
        printf("\n x%d=%f\n",i,x[i]);
    }
    return(0);
}

Input/Output:

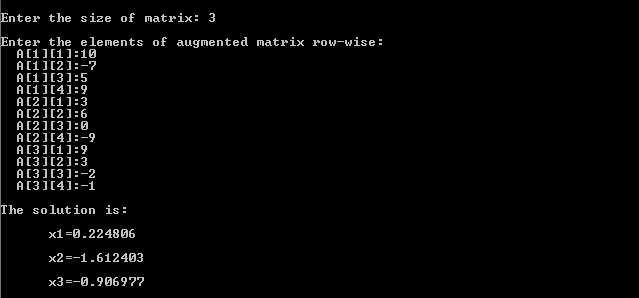
Note: Let us consider a system of 10 linear simultaneous equations. Solving this by Gauss-Jordan method requires a total of 500 multiplication, where that required in the Gauss elimination method is only 333.

Therefore, the Gauss-Jordan method is easier and simpler, but requires 50% more labor in terms of operations than the Gauss elimination method. And hence, for larger systems of such linear simultaneous equations, the Gauss elimination method is the more preferred one. Find more information about the two methods here.

Algorithm and Flowchart

Gauss Jordan method is commonly used to find the solution of linear simultaneous equations. In science and engineering, it is used to find the output of a chemical plant, examine a network under sinusoidal steady rate, etc.
Here’s a simple algorithm for Gauss Jordan Method along with flowchart, which show how a system of linear equations is reduced to diagonal matrix form by elementary row operations. The solution is directly and conveniently obtained by this method but requires a little more calculation.
Gauss Jordan method is a modified version of the Gauss elimination method. The Gauss Jordan algorithm and flowchart is also similar in many aspects to the elimination method. Compared to the elimination method, this method reduces effort and time taken to perform back substitutions for finding the unknowns.
In Gauss Elimination, the unknown variables are eliminated from the pivotal equation only, but in Gauss Jordan method, they are eliminated from all the equations. Before going through the algorithm and flowchart, learn how matrix is diagonalized in Gauss Jordan method?

Gauss Jordan Method Algorithm:

• Start
• Read the order of the matrix ‘n’ and read the coefficients of the linear equations.
• Do for k=1 to n
  Do for l=k+1 to n+1
  a[k][l] = a[k][l] / a[k][k]
  End for l
  Set a[k][k] = 1
  Do for i=1 to n
  if (i not equal to k) then,
  Do for j=k+1 to n+1
  a[i][j] = a[i][j] – (a[k][j] * a[i][k])
  End for j
  End for i
  End for k
• Do for m=1 to n
  x[m] = a[m][n+1]
  Display x[m]
  End for m
• Stop

Gauss Jordan Method Flowchart:

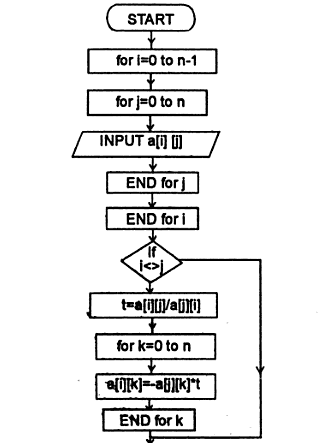
The flowchart is continued after “END for k”.

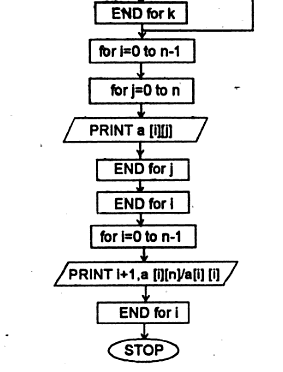
Here is another flowchart for Gauss Jordan method.

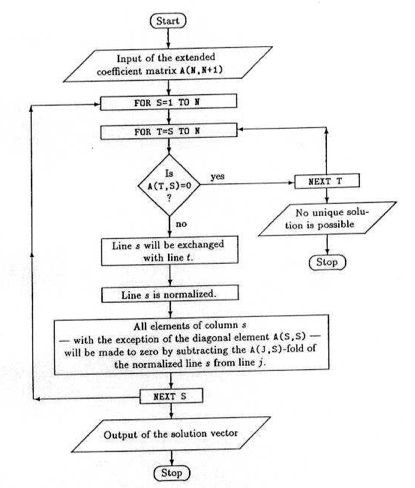
The aforementioned algorithm and flowchart seem simple, but Gauss Jordan method is generally considered to be a bit tedious in terms of additional calculation. Additionally, this method proves to be a effective one for a smaller system of linear simultaneous equations.
If you consider a system of 10 or 20 such equations, 500 multiplications would be required to solve the system using Gauss Jordan method. But, if you adopt Gauss Elimination method the number of multiplications required is only 333. So, Gauss Jordan is the simpler method, but requires 50% more calculation compared to the elimination method.