Euler’s Method

C Program

Solving an ordinary differential equation (ODE) or initial value problem means finding a clear expression for y in terms of a finite number of elementary functions of x. Euler’s method is one of the simplest method for the numerical solution of such equation or problem. This C program for Euler’s method considers an ordinary differential equations, and the initial values of x and y are known.
Mathematically, here, the curve of solution is approximated by a sequence of short lines i.e. by the tangent line in each interval. (Derivation) Using these information, the value of the value of ‘yn’ corresponding to the value of ‘xn‘ is to determined by dividing the length (xn – x) into n strips.

Therefore, strip width= (xn – x)/n and xn=x0+ nh.
Again, if m be the slope of the curve at point, y1= y0 + m(x0 , yo)h.
Similarly, values of all the intermediate y can be found out.

Below is a source code for Euler’s method in C to solve the ordinary differential equation dy/dx = x+y. It asks for the value of of x0 , y0 ,xn and h. The value of slope at different points is calculated using the function ‘fun’. The values of y are calculated in while loop which runs till the initial value of x is not equal to the final value. All the values of ‘y’ at corresponding ‘x’ are shown in the output screen.

Source Code for Euler’s Method in C:

#include
float fun(float x,float y)
{
    float f;
    f=x+y;
    return f;
}
main()
{
    float a,b,x,y,h,t,k;
    printf("\nEnter x0,y0,h,xn: ");
    scanf("%f%f%f%f",&a,&b,&h,&t);
    x=a;
    y=b;
    printf("\n  x\t  y\n");
    while(x<=t)
    {
        k=h*fun(x,y);
        y=y+k;
        x=x+h;
        printf("%0.3f\t%0.3f\n",x,y);
    }
}

Input/Output:

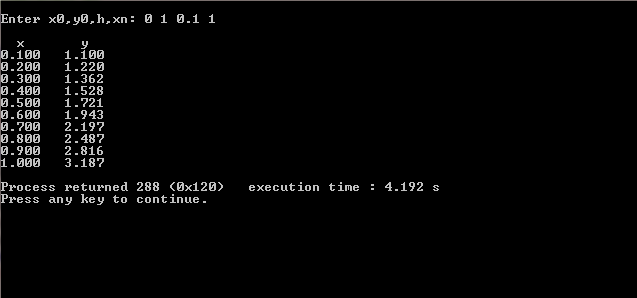
Euler’s method is unarguably very very simple, but it cannot be considered as one of the best approach for to find the solution of initial value problems. It is considered to be very slow, and hence it was later modified in the name of Modified Euler’s Method. The Euler’s method code code in this post needs to be compiled in Code::Blocks. It is well-tested and is bug-free. Any questions related to Euler’s method, or its source code in C presented above, can be mentioned and discussed in the comments.

MATLAB Program

Euler’s method, named after Leonhard Euler, is a popular numerical procedure of mathematics and computation science to find the solution of ordinary differential equation or initial value problems. It is a first order method in which local error is proportional to the square of step size whereas global error is proportional to the step size.
Considered the simplest method to solve ordinary differential equation, Euler’s method finds a clear expression for y with respect to a finite number of elementary functions of x. Here, the initial values of x and y are already known.
The algorithm/flowchart and C program. of this method has already been discussed in earlier tutorials. Here’s a program code for Euler’s method in MATLAB along with its mathematical derivation and numerical example.

Derivation of Euler’s Method:

Euler’s method is basically derived from Taylor’s Expansion of a function y around t0. The equation to satisfy this condition is given as:
y(t0 + h) = y(t0) + hy’(t0) + ½ h2 y’’ (t0) + 0 ( h3 )
As per differential equation, y’ = f( t, y). Substituting this in Taylor’s Expansion and neglecting the terms with higher order (or power), we get:
y’(t0) = [y( t0 + h) – y(t0)]/ h
which is the forward finite difference formula of Euler’s method.

Consider an initial value problem as below:
y’(t) = f(t, y(t)), y(t0) = y0
In order to find out the approximate solution of this problem, adopt a size of steps ‘h’ such that:
tn = t n-1 + h and tn = t0 + nh.
Now, it can be written that:
yn+1 = yn + hf( tn, yn).
The value of yn is the approximation of solution to the ordinary differential equation (ODE) at time tn. This approach is used to write the program for Euler’s method in Matlab.

Euler’s Method in MATLAB:

2
3
4
5
6
7
8
9
10
11
12
13
%function t=t(n,t0,t1,y0)
 
function y=y(n,t0,t1,y0)
h=(t1-t0)/n;
t(1)=t0;
y(1)=y0;
for i=1:n
t(i+1)=t(i)+h;
y(i+1)=y(i)+h*ex(t(i),y(i));
end;
V=[t',y']
plot(t,y)
title(' Euler Method')

This code for Euler’s method in Matlab finds out the value of step size (i.e. h) on the basis of initial and final value given in the problem and the total number of iteration. After that, each intermediate values of y are estimated based on Euler’s equation.
Finally, the program finds the required value of y. Here’s a sample screenshot of this program on MATLAB’s Command Window.

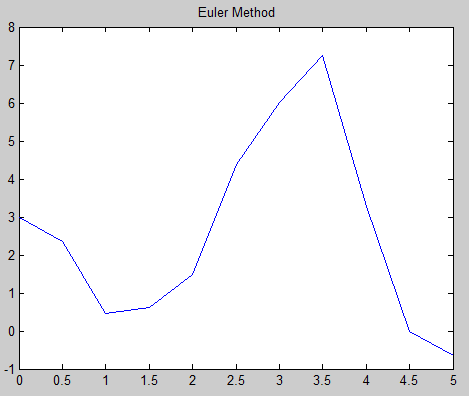
The screenshot below is the graphical output of Euler’s MATLAB program.

How to run program of Euler’s method in MATLAB?

• Copy the aforementioned source code to a new MATLAB file and save it as m. For example: euler.m.
• Create another MATLAB file, named ex.m. The file must contain the function to be approximated in standard MATLAB syntax. For example, if y = (t2 – x2) sinx is to be solved, the content of ex.m file will be:

%x is a function of t and y is the first derivative x'(t)
 
function y=y(t,x)
y=(t^2-x^2)*sin (x);

• Go to MATLAB command window, and write euler(n, t0, t1, y0) and return, where y(t0) = y0 is the initial condition, t0 and t1 are the initial and final points, and n is the number of t-values.
• Finally, the graph of the problem along with the numerical solution (as shown in the two screenshots above) will be displayed.

Euler’s Method Numerical Example:

As a numerical example of Euler’s method, we’re going to analyze numerically the above program of Euler’s method in Matlab. The question here is:

y’ = y, y(0) = 1

Choose the size of step as h = 1. The equation used in Euler’s method is:
yn+1 = yn + h f( tn, yn)
where, f( tn, yn) = y
Now,
f( t0, y0 ) = f( 0, 1) = 1
h f(y0) = 1 * 1 = 1
Again,
y 0 + h f(y0) = y1 = 1 + 1 * 1 = 2
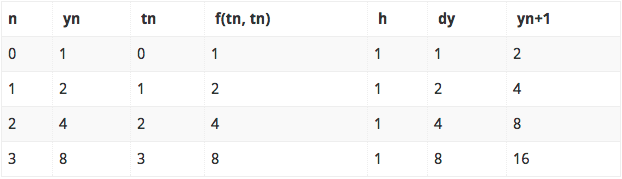
Repeating above steps for y2, y3 and y4 :
y 2 = y1 + h f(y1) = 2 +1 * 2 = 4
y 3 = y2 + h f(y2) = 4+1 * 4 = 8
y 4 = y3+ h f(y2) = 8 +1 * 8 = 16
All these calculation can be presented in a tabular format:

Finally, the graphical representation of this problem is given below:

If you have any questions regarding Euler’s method, its MATLAB code, or anything else relevant, bring them up from the comments section below. You can find more Numerical methods tutorial using MATLAB here.

Algorithm and Flowchart

Euler’s method is considered to be one of the oldest and simplest methods to find the numerical solution of ordinary differential equation or the initial value problems. Here, a short and simple algorithm and flowchart for Euler’s method has been presented, which can be used to write program for the method in any high level programming language.
Through Euler’s method, you can find a clear expression for y in terms of a finite number of elementary functions represented with x. The initial values of y and x are known, and for these an ordinary differential equation is considered.
Now, lets look at the mathematics and algorithm behind the Euler’s method. A sequence of short lines is approximated to find the curve of solution; this means considering tangent line in each interval. Using the information obtained from here, the value of ‘yn’ corresponding to the value of ‘xn‘ is to determined by dividing the length (xn – x) into n intervals or strips.
So, strip width= (xn – x)/n and xn=x0+ nh.
Again, if m be the slope of the curve at point, y1= y0 + m(x0 , yo)h.
Now, from this all the intermediate ‘y’ values can be found. This method was developed by Leonhard Euler.

Euler’s Method Algorithm:

• Start
• Define function
• Get the values of x0, y0, h and xn
  *Here x0 and y0 are the initial conditions
  h is the interval
  xn is the required value
• n = (xn – x0)/h + 1
• Start loop from i=1 to n
• y = y0 + h*f(x0,y0)
  x = x + h
• Print values of y0 and x0
• Check if x < xn
  If yes, assign x0 = x and y0 = y
  If no, goto 9.
  
• End loop i
• Stop

Euler’s Method Flowchart:

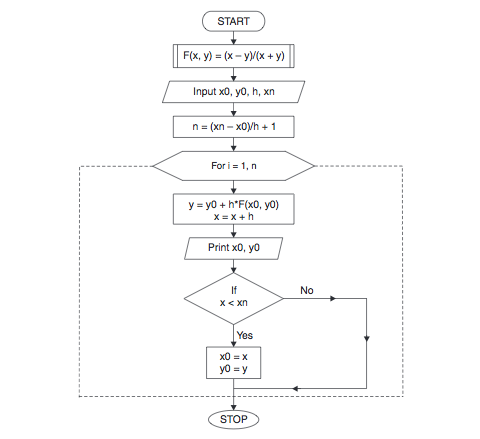
Euler’s method is very simple and easy to understand and use in programming to solve initial value problems. You can refer the aforementioned algorithm and flowchart to write a program for Euler’s method in any high level programming language.
Note: Euler’s method cannot be regarded as one of the best approaches to solve ordinary differential equations. It is very slow, but its modified form, Modified Euler’s Method is fast.