JPEG Display Process page-3

Introduction

We have before us a wealth of 24-bit, true-color imagery that includes everything from public domain clip art to reproductions of the Renaissance masters on CD-ROM. Today’s 24-bit video display adapters can render them in 16.7 million vibrant colors, bringing true photorealism to our desktop computers. The images are wonderful, but ¼

The problem is that most of our desktop computers are only capable of displaying a palette of 256 colors. A year or so ago, 24-bit color display technology cost nearly as much as the computer itself. Even today, 24-bit display adapters remain relatively expensive, and few of us can afford to upgrade or replace our hardware every six months -- maybe next year, we keep on telling ourselves. Until then, we will have to make do with what we have.

Actually, 256 colors are often all we really need. The human eye can distinguish at best several hundred thousand colors, and most scenes contain surprisingly few of these. An abundance of 256-color images has demonstrated that we can achieve photorealism -- or something close to it -- with nothing more sophisticated than a judicious selection of colors.

Our saving grace is that most 256-color display adapters have programmable palettes. All IBM-PC VGA and SuperVGA adapters, for example, are capable of generating at least 262,144 colors in their lower resolution modes. However, only 256 of these can be selected for display at a time, and so 8-bit graphics file formats such as BMP or PCX must include a palette header that tells the display software how the palette should be programmed.

This leaves us with the following problem: we need to 1) analyze a 24-bit color image; 2) select the colors that best represent it; and 3) create an equivalent bitmap image with 256 or fewer colors that we can display. For this, we need a utility program, or more generally, an appropriate algorithm.

While there are several algorithms we can choose from, they all perform some sort of color quantization. Simply stated, this technique groups similar pixel colors and replaces them with a single “quantized” color that represents their average red, green and blue primary color components. The quality of the resultant image will vary, depending on both the number of distinct colors in the original image and how intelligently the algorithm identifies and groups “similar” colors.

We can visualize this process by arranging our 16.7 million possible colors into an RGB color cube, shown in outline in Figure 1. Starting from the “black” vertex, each axis represents one of the primary colors -- red, green or blue. Having 8 bits per primary color, we divide these axes into 256 segments. If the color cube is similarly divided, each possible color is represented by one of 16.7 million (256´256´256) subcubes.

More generally, we can imagine a hierarchy of nested subcubes. Figure 2, for example, shows the color cube uniformly divided into eight equal subcubes, where each one serves to group approximately similar colors. Each of these subcubes can be similarly divided, resulting in 16.7 million indivisible subcubes after only eight iterations.

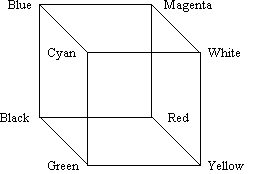/> Figure 1 - RGB color cube

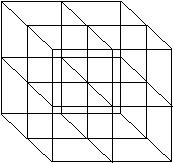
Figure 2 - Division into 8 subcubes

From this, we can derive a simple algorithm called uniform quantization that divides the color cube into a fixed number of equally sized subcubes. Dividing each axis into four segments, for example, groups the original colors into one of 64 subcubes. The “quantized” color for any pixel whose original color lies within a given group is then the average color of all pixels within that group.

Unfortunately, this approach often results in poor image quality. Color bands are often visible on what should be smoothly shaded surfaces, making the images appear posterized. This is particularly true for portraits, where we expect to see subtle gradations of color in skin tones.

The basic problem is that we are allocating colors for our palette that may not occur in a given image. We can usually do much better by analyzing the image more carefully. If there is a preponderance of skin tones, for example, it makes sense to finely subdivide the color cube in the region of these colors. Other, less frequently occurring colors can be represented by larger subcubes.

Heckbert [1992] introduced two algorithms that follow this line of reasoning. His popularity algorithm chooses the most frequently occurring colors to represent all the colors in the original image, while his median cut algorithm selects colors such that each represents approximately the same number of pixels in the quantized image. Unfortunately, the image quality produced by popularity quantization depends on the number and distribution of colors in the original image, and both algorithms require sufficient memory to store counters for each original color. An 800´600 pixel image, for example, may require almost two megabytes of memory if each pixel has a slightly different color. While the median cut algorithm usually produces good quality images, it is ill-suited for personal computers with limited memory resources.

This brings us to the algorithm of choice, octree quantization. Introduced by Gervautz and Purgathofer [1990], it requires very little memory, is reasonably fast, and produces good quality images that are comparable to those produced by the median cut algorithm. Best of all, it can be easily implemented on a microcomputer under MS-DOS and its stringent memory restrictions.

Color Quantization – Octree

The octree quantization algorithm is based on the representation of the RGB subcube hierarchy as an octree data structure, a tree where each node has eight child nodes. The tree itself has nine levels, corresponding to the root node (level 0) and the eight bits used to represent each primary color. Each intermediate node represents a subcube and a corresponding group of colors. The leaf nodes–all 16.7 million of them–represent the individual 24-bit colors.

We fortunately do not need to store the entire octree in memory. Instead, we only need to store those leaf nodes that represent the quantized colors and the intermediate nodes that lead to them from the tree’s root. As such, the octree will always be mostly incomplete. It can be shown that for k quantized colors, we need a maximum of k leaf and k‑1 intermediate nodes. Assuming (say) 64 bytes per node, a 256‑color octree occupies less than 32 kilobytes of RAM.

Consider a single 24-bit color: it consists of three 8-bit bytes, one for each primary color. The most significant bit of each byte divides each axis of the RGB color cube into two segments, and so the color cube itself is partitioned into eight equal subcubes. Examining these three bits determines which subcube and associated intermediate node the color belongs to. Repeating this process for the next most significant bit of each byte places the color in the next level of the octree hierarchy, and so on. The combination of the three least significant bits determines the exact 24-bit color and its leaf node.

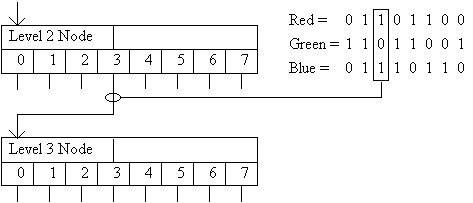
Figure 3 - Determining a child node from color bits

The point is that each of these colors defines a unique path through the octree from the root to the leaf nodes. We can add a color to the octree by tracing its path and allocating new nodes from memory as necessary. More importantly, colors that have been grouped will share a common path to some intermediate node. We can limit the number of leaf nodes by cutting the tree at this node and designating it as a leaf; its child nodes can then be deleted. The process is called octree reduction.

Ignoring the details for the moment, we can see that octree color quantization is a two-pass procedure. In the first pass, we sequentially examine each pixel of a 24-bit color image and, if necessary, insert its color into our octree data structure. We perform octree reduction whenever the number of inserted colors (that is, the current number of leaf nodes) exceeds our predetermined limit k. (While we will normally choose this value to be 256, it can be made larger or smaller as needed.)

Once we have completed our examination of the image, we know that the octree will contain a maximum of k leaf nodes. Again ignoring the details, we can calculate an average color for each of these nodes and use them to initialize the color palette header of our equivalent graphics file.

The second pass consists of reading the image pixels again. This time, however, each pixel color is guaranteed to define an existing path through the octree to a leaf node. The average or exact color associated with this node represents the quantized color for the pixel. This allows us to map the original 24-bit pixel colors to our set of k display colors.

Pass One - Building the Octree

Building the octree data structure is a straightforward procedure that is performed by the module BuildTree, which calls the module GetPixel to sequentially examine the image pixels. Since only their colors are important, the pixels themselves can be examined in any convenient order. The first k distinct colors are entered by the recursive module InsertNode as exact representations at level 8 in the octree node hierarchy. The module FindChild determines the appropriate child node at each level according to the bit pattern of the three primary color values.

A pixel count is maintained for each node. As the path of each pixel color is traced through the hierarchy, the count for each associated node is incremented by InsertNode. New nodes are dynamically allocated by the module MakeNode from memory and added to the tree only when the current pixel color defines a new path.

A node is “reducible” if it has more than one child node. The module MakeReducible is called by InsertNode to add such nodes to a linked linear list, with one list for each intermediate node level of the octree hierarchy. The nodes are marked to ensure that they are not added to their respective lists more than once as new child nodes are created.

If there are k or fewer distinct colors in the entire image, then each color can be represented exactly, and nothing further needs to be done. More often, however, we will need to repeatedly perform octree reduction by calling the module ReduceTree to limit the number of leaf nodes. This function finds the next reducible intermediate node, recursively deletes its children with the module DeleteNode, and marks it as a new leaf.

The purpose of octree reduction is to group similar colors. Any intermediate node with two or more children is a candidate for cutting and marking as a new leaf node. However, those intermediate nodes with the largest depth represent paths to colors that are closest to one another, and so these should be cut first. The module GetReducible therefore starts searching the linked lists of reducible nodes at the largest depth, and continues upwards until it finds the first non-empty list.

Now, suppose there is more than one reducible node at the largest depth. Which one we choose is a good question. Gervautz and Purgathofer [1990] suggested two options. First, we can choose the node that represents the smallest number of pixels. This will tend to minimize the total image error and preserve subtle gradations across smoothly shaded surfaces. Alternatively, we can choose the node with the largest pixel count. This will tend to result in large areas having slightly different fill colors and more visible color banding. However, shading details, particularly anti-aliasing, will remain mostly intact. (Note that these results are not guaranteed, since the pixel counts are representative only of the pixels examined so far.) GetReducible opts for the latter by choosing the node with the largest pixel count.

It must also be noted that node reduction always occurs at the current “reduction level” of the largest depth intermediate nodes. That is, node reduction begins at level 7 and may move upwards while the octree is being built. The insertion of new colors must stop at the level immediately below the current reduction level (the current “leaf level”) to prevent the possibility of existing color groups being split.

Finally, we need to determine the average color of each node. This is most easily done by summing the RGB colors for those pixels whose paths include the node (the module AddColor). The average color is then the sum of each primary color divided by the node’s pixel count.

Color Palette Initialization

Given a completed octree, we can now initialize the color palette. Each leaf node of the octree represents a quantized RGB display color. The module FillPalette recursively traverses the octree looking for these nodes. When it finds one, it calls the module GetColor to calculate the average pixel color and copies the result to the static array Palette. The current array index is then stored in the leaf node for later use.

The module FillPalette is called by the module InitPalette, which is typically responsible for transforming Palette into the palette information required by the graphics file format. The Microsoft BMP file format, for example, has a reserved byte in each RGB entry that must be zeroed. In other cases, such as the PCX file format, the palette can be copied as is.

Pass Two - Mapping the Colors

The second pass of the octree quantization algorithm consists of mapping each 24-bit pixel color in the original image to its quantized display color. This is done by calling the module QuantizeColor to perform a recursive depth-first traversal of the octree for each pixel, using its original color as the search key. This search is guaranteed to end at a leaf node at some depth, which provides the previously saved palette entry index for the pixel’s quantized color. If the node is at depth 8, the color is an exact representation of the original. Otherwise, it is the average color of all the pixels whose paths lead to the node.

With this, we have all the information we need to complete our equivalent bitmap graphics file. In most cases, a graphics file with a color palette represents the color of each pixel in the file by its palette entry index. There may be some extra work involved in compressing the pixels (the PCX file format, for instance, uses run-length encoding for 8-bit color images), but the color quantization is complete.

Problems and Solutions

The octree color quantization algorithm is not without its problems. In particular, it will alleviate but not eliminate the color banding effects that uniform quantization generates. In some cases, it may be necessary to incorporate color dithering (e.g., Thomas and Bogart [1991]) before quantizing an image -- the random noise tends to mask any color bands. Color “jittering” (Bragg [1992]) is another approach that is useful when a series of images are to be incorporated into a video sequence. Unlike color dithering, jittering ensures that the random noise pattern remains constant between images, eliminating the grainy “snow” effect that would otherwise occur when the video is played.

We can also do better in terms of color quantization. Xiang and Joy [1994] offer a generalization of the octree method, called “agglomerative clustering”, that produces less color banding. However, its memory requirements depend on the number of original rather than quantized colors. As such, it may require memory in excess of that available to MS-DOS without a memory extender.

All in all, Gervautz and Purgathofer’s octree color quantization algorithm is a useful tool for any computer graphics programmer, at least until we can all afford 24-bit color display technology.