How Floats Are Stored

Any elementary book on computers would tell you how integers are stored in memory. However, these books conveniently skip the topic of storage of floats and doubles. Even most C books just tell us that floats are 4 bytes long whereas doubles are 8-byte entities. But the question as to what is exactly present in these 4/8 bytes is largely unanswered. In this article we would explore the commonly used storage method for floats and doubles. Floats and doubles are stored in mantissa and exponent form except that instead of the exponent representing the power of 10, it represents a power of 2, since base 2 is computer's natural format. The number of bytes used to represent a floating-point number depends on the precision of the variable. float is used to declare single-precision variables, whereas the type double denotes double-precision values. The representation of the mantissa and exponent in these variables is in accordance with the IEEE floating point standards. This representation is followed by most of the C compilers. The IEEE format expresses a floating-point number in a binary form known as nomalised form. Normalisation involves adjusting the exponent so that the binary point (the binary analog of the decimal point) in the mantissa always lies to the right of most significant nonzero digit. In binary representation, this means that the most significant digit of the mantissa is always a 1. This property of the normalised representation is exploited by the IEEE format when storing the mantissa. Let us consider an example of generating the normalised form of a floating point number. Suppose we want to represent the decimal number 5.375. Its binary equivalent can be obtained as shown below:

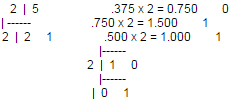
Writing remainders in Writing whole parts in the same
reverse order we get 101 order in which they are obtained
we get 011

Thus the binary equivalent of 5.375 would be 101.011. The normalised form of this binary number is obtained by adjusting the exponent until the decimal point is to the right of most significant 1. In this case the result is 1.01011 x 22 .The IEEE format for floating point storage uses a sign bit, a mantissa and an exponent for representing the power of 2. The sign bit denotes the sign of the number: a 0 represents a positive value and a 1 denotes a negative value. The mantissa is represented in binary. Converting the floating-point number to its normalised form results in a mantissa whose most significant digit is always 1. The IEEE format takes advantage of this by not storing this bit at all. The exponent is an integer stored in unsigned binary format after adding a positive integer bias. This ensures that the stored exponent is always positive. The value of the bias is 127 for floats and 1023 for doubles. Thus, 1.01011 x 22 is represented as shown below:

Let us take another example. Suppose we want to represent the number -0.25 in IEEE format. On conversion to binary this number would become -0.01 and in its normalised form it would be -1.0 x 2-2. This normalised form when represented in IEEE format it would look like:

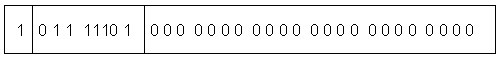
sign exponent-obtained after mantissa stored in normalised form
bit adding a bias 127 to
exponent -2

Now we know that converting the floating-point number to its normalised form results in a mantissa whose most significant digit is always 1. The IEEE format takes advantage of this by not storing this bit at all. The exponent is an integer stored in unsigned binary format after adding a positive integer bias. This ensures that the stored exponent is always positive. The value of the bias is 127 for floats and 1023 for doubles. The following figure shows how any general float or double is represented in IEEE format.

IEEE float representation

IEEE double representation

Most C books tell you that the valid range for floats is 10-38 to 1038. Have you ever thought how such an odd range is used? Well, the answer lies in the IEEE representation. Since the exponent of a float in IEEE format is stored with a positive bias of 127, the smallest positive value that you can store in a float variable is 2-127, which is approximately 1.175 x 10-38. The largest positive value is 2128, which is about 3.4 x 1038. Similarly for a double variable the smallest possible value is 2-1023, which is approximately 2.23 x 10-308. The largest positive value that can be held in a double variable is 21024, which is approximately 1.8 x 10308. There is one more quirk. After obtaining the IEEE format for a float when time comes to actually store it in memory it is stored in the reversed order. That is if we call the four byte IEEE form as ABCD then while storing in memory it is stored in the form DCBA. Let us understand this with an example. Suppose the floating-point number in question is 5.375. Its IEEE representation is 0100 0000 1010 1100 0000 0000 0000 0000. Expressed in hex this is 40 AC 00 00. While storing this in memory it is stored as 00 00 AC 40. How do we confirm this? How else but through a program. Here it is...

main( ) { float a = 5.375 ; char *p ; int i ;

p = ( char * ) &a ; for ( i = 0 ; i <= 3 ; i++ ) printf ( "%02x ", ( unsigned char ) p[i] ) ; }

All that we have done is set up a character pointer which points to the first byte of the four byte float. Next through this pointer we have accessed and printed the values in each of the four bytes of the float. I am sure you would be able to write a similar program for printing the values in individual bytes of a double variable. The representation of a long double (10 byte entity) is also similar. The only difference being unlike the float and double the most significant bit of the normalised form is specifically stored. In a long double one bit is occupied by sign, 15 bits by the biased exponent (bias value 16383) and 64 bits by the mantissa.