JPEG Baseline Compression Page-2

JPEG Baseline Compression

As mentioned above JPEGs usually throw out 3/4 of the chrominance information. The header of the JPEG file contains a horizontal & a vertical sample factor for each component. The luminance(Y) component is always sampled at full resolution i.e. a value is stored for each pixel. Typically, but not always, the horizontal & vertical sample factors for Y are 2 and the horizontal & vertical sample factors for both of the chrominance componentas are 1. For this case each block of 4 pixels would be sampled with four values for Y and only one each for U & V.

The largest horizontal & vertical sample factors determine the height & width of the Minimum Coded Unit (MCU) respectively. For the case of figure the MCU would be two 8x8 blocks high & two 8x8 blocks wide for a total of four 8x8 blocks. The blocks are stored in the file all Ys first then all Us then all Vs. For this case one MCU would contain four Y 8x8 blocks followed by one U 8x8 block & one V 8x8 block.

The National Imagery Transmission Format Standard (NITFS) From the Department of Defense (DOD) MIL-STD-188-198A Section 5.1.1.1 States the following:

"The encoding process shall add samples as necessary at the right and bottom edges of the image to guarantee an integral number of blocks . When an image does not contain enough data to fill an 8x8 block along the rightmost or bottom edge, the sample values in the rightmost and/or bottom edges shall be replicated in the extra space to add columns to the right and rows to the bottom. The decoding process shall use header information from the interchange format to identify any such additional samples and remove them."

In my test file testimg.jpg, the width is 150 pixels. 19 x 8 = 152 so it would seem from the above statement that the width should be 152. But, when I tried to display it using a width of 152, the pixels did not line up correctly. An integral number of MCUs would give 10 x 16 = 160. With a width of 160, the pixels lined up correctly. So, apparently, there is actually an integral number of MCUs instead of an integral number of 8x8 data units.

Step 3 : The following steps are taken for compressing each 8x8 block of MCU.

As mentioned above the image is broken down into 8x8 blocks of pixels. The 8x8 blocks are then combined into Minimum Coded Units or MCUs. The image is then processed one MCU at a time. Within the MCU each component is processed separately one 8x8 block at a time. The component blocks are processed all Ys first then all Us then all Vs.

Step a: Shift the block

The block is shifted from numbers 0 - 255 to numbers -128 to 127 by subtracting 128. This is done because a uniformly distributed block would then give a zero DC coefficient after the DCT.

118 91 123 125 124 114 117 104 -10 -37 -05 –03 -04 -14 -11 -24

100 93 88 85 87 100 115 105 -28 -35 -40 -43 -41 -28 -13 -23

94 101 78 99 112 87 109 115 -34 -27 -50 -29 -16 -41 -19 -13

104 82 83 78 92 118 124 88 -24 -46 -45 -50 -36 -10 -04 -40

119 93 99 104 76 111 86 112 -09 -35 -29 -24 -52 -17 -42 -16

83 119 104 92 111 76 112 100 -45 -09 -24 -36 -17 -52 -16 -28

97 85 90 100 106 125 123 86 -31 -43 -38 -28 -22 -03 -05 -42

99 86 85 105 81 99 115 119 -29 -42 -43 -23 -47 -29 -13 -09

64 Component amplitudes The 64 amplitudes shifted down by 128

Step b: Perform a FDCT (Forward Discrete Cosine Transform) on the block

The ideas behind JPEG compression come from an engineering background. Electrical and sound waves can be repersented as a series of amplitudes over time. A continuous tone image can be represented as a series of amplitudes, for each color component, over 2 dimemsional space. A Discrete Cosine Transform, related to the Fourier Transform is used to discard higher frequency information that has little visual effect on the image.

In the 64 input pixels (from the 8x8 block), it compares the color data but not the intensity level of each pixel to its neighbors. If the difference between the pixels is large (i.e. a color jump), then the DCT will produce a large discrete coefficient for that pixel. If the difference is small (i.e. a gradual color change), it will produce a small DC coefficient. At the end of the computation, we have 64 DC coefficients of varying sizes. An average sampling of DC coefficients would produce some large, medium and small DC coefficients Recall that the large amplitudes signify a large color difference. The term for this is that the pixels have been mapped from the spatial domain into frequency-space.

This is where the founding principle of JPEGs returns-- the human eye cannot perceive subtle color changes. In frequency-space, this maps to the smaller DC coefficients. Therefore, we can eliminate or round to zero the smaller DC coefficients and keep only the medium and larger DC coefficients, which is the data that is most important anyway. This is the second portion of the algorithm that results in a lossy technique. However, the user is allowed a degree of control over the amount of loss (which corresponds directly to file size).

If you start with an 8x8 block of 64 values, f(x,y), they can be transformed to a new set of 64 values, F(x,y), by the Forward Discrete Cosine Transform and then back to the original 64 values, f(x,y), by the Inverse Discrete Cosine Transform. The equations for the Discrete Cosine Transforms are:

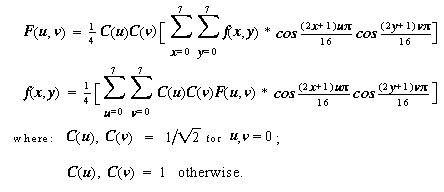
The Forward Discrete Cosine Transform creates 64 coefficients. The first coefficient in the upper right hand corner is for zero frequency and, to borrow terminology from electronics, is called the DC coefficient. The others are called AC coefficients.

-217.625 -32.686 15.582 16.972 -1.376 21.802 -7.132 2.729

15.022 5.594 -3.423 3.416 7.983 -1.074 3.717 10.550

21.737 -8.150 -13.483 -6.075 6.168 13.366 -0.490 3.289

23.404 24.748 -19.724 -10.992 -5.045 -3.321 7.425 9.585

12.124 4.600 4.754 4.605 6.875 20.625 30.096 -12.687

14.610 -9.347 -27.242 27.260 -9.347 7.631 -4.987 14.890

10.343 6.876 -4.990 -29.439 16.523 -18.653 -24.266 11.388

13.292 6.131 -5.968 -2.067 20.673 1.179 14.921 -16.733

64 coefficients after the FDCT

Step c: Quantize the block

Next the block is quantized using a quantization table. Quantization means that each coefficient is divided by an integer between 1 & 255 and rounded to the nearest integer. The quantization table is chosen to reduce the precision of each coefficient to no more than necessary. The choice of the quantization table is a trade off between compression achieved & images quality. This quantization table is stored in the file header for use by the decompressor, which multiplies each coefficient by the same number.

Formula: ( Round to nearest integer)

Quantized Value ( a, b) = DCT (a,b) / Quantization Table value (a,b)

8 6 6 7 6 5 8 7 -27 -5 2 2 0 4 0 0

7 7 9 9 8 10 12 20 2 0 0 0 0 0 0 0

13 12 11 11 12 25 18 19 1 0 -1 0 0 0 0 0

15 20 29 26 31 30 29 26 1 1 0 0 0 0 0 0

28 28 32 36 46 39 32 34 0 0 0 0 0 0 0 0

44 35 28 28 40 55 41 44 0 0 0 0 0 0 0 0

48 49 52 52 52 31 39 57 0 0 0 0 0 0 0 0

61 56 50 60 46 51 52 50 0 0 0 0 0 0 0 0

Quantization Table 64 Quantized Coefficients

In this example, we have defined some constant below which all coefficients are rounded to zero and discarded. Here is where the user gains control. This is typically done when you save the file to a JPEG from your graphics program. The program should present a slider giving you a range of image qualities that go from low to high. This slider is, in effect, moving the red line in the example up for lesser quality (and smaller file size) and down for greater quality (and larger file size). Remember that moving the red line up will result in more coefficients being below the line and therefore rounded to zero and discarded.

Note that there is a point at which the compressed file is of such degraded quality to be considered useless. Depending on the image contents, this will lie from 70% to 90% compression.

Step d: Subtract the last DC coefficient from the current DC coefficient

Next the last DC coefficient is subtracted from the current DC coefficient. (Unless it is the first DC coefficient in the image). This is done because the coefficients are stored in variable-length binary numbers. So we want the coefficients to be as small as possible.

Step e: Zigzag the block

To set up the quantised data for the Entropy encoding procedure, the current matrix format is not particularly useful. Since the quantised coefficients have a greater chance of being zero as the order of the spatial frequency values increases it would be beneficial to arrange the coefficients in this order. I.e. to somehow arrange the coefficients so that the data was in a one-dimensional array sorted from the DC value to the highest order spatial frequency (8,8). This is done by zig-zag ordering. The following diagram illustrates the sorting algorithm. Next the block is rearranged in zigzag order. This usually increases the run length of zeros.