JPEG Baseline Compression Page-3

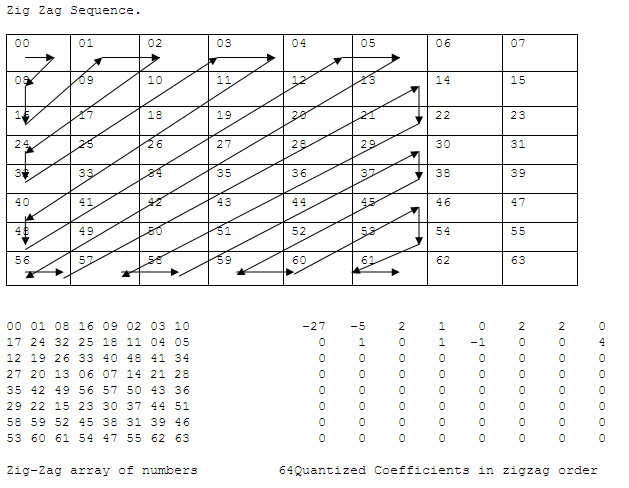
Step f: Zero run length encode the block

Next the block is zero run length encoded as follows:

-27 0 -5 0 2 0 1 1 2 0 2

2 1 1 1 0 -1 2 4 0 0

This sting of numbers is interpreted as:

• 1 The DC coefficient is -27
• 2 An AC coefficient of -5 preceeded by no zero value AC coefficients
• 3 An AC coefficient of 2 preceded by no zero value AC coefficients
• 4 An AC coefficient of 1 preceded by no zero value AC coefficients
• 5 An AC coefficient of 2 preceded by 1 zero value AC coefficients
• 6 An AC coefficient of 2 preceded by no zero value AC coefficients
• 7 An AC coefficient of 1 preceded by 2 zero value AC coefficients
• 8 An AC coefficient of 1 preceded by 1 zero value AC coefficients
• 9 An AC coefficient of -1 preceded by no zero value AC coefficients
• 10 An AC coefficient of 4 preceded by 2 zero value AC coefficients
• 11 The rest of the block is zero value AC coefficients

Compare this with the 64 Quantized Coefficients in zigzag order above.

Step g: Break down the non-zero coefficients into variable-length binary numbers & their lengths

Next the coefficients in the above string of numbers are converted into variable-length binary numbers. The numbers are then stored as a length followed by a variable-length binary number.

• · Positive numbers always start with a 1 and are coded in the usual binary fashion e.g. 5 would be stores as 101 which has a length of 3 bits. (no leading zeros are stored)
• · Negative numbers always start with a 0. to get the number adds one and left fill the integer with 1s. e.g. 0101 + 1 = 0110 then left filled with 1s 1111 0110 = -10 decimal as a signed number.

Step h: Entropy encode the run lengths & binary number lengths

Next the zero run lengths are combined with the bit length of the AC coefficients. Upper nibble = run length, lower nibble = bit length. e.g. 2 4, An AC coefficient of 4 preceded by 2 zero value AC coefficients, above, would be 0010 0100 or in hexadecimal 0x24.

There are a couple of special cases.

• 1. When both the zero run length & the AC coefficient bit length are zero it means the rest of the block has zero value AC coefficients.
• 2. When the zero run length is 15 & the AC coefficient bit length is zero it means a zero run length of 16 & no non-zero AC coefficient.

Then the DC coefficient (difference from last DC coefficient) bit lengths & the combined AC coefficient bit length & zero run lengths are entropy encoded. Entropy encoding uses shorter bit length codes to represent more common codes and longer bit length codes to represent less common codes. JFIF uses Huffman Coding for entropy encoding.

For Huffman coding: Given a set of symbols and the probability of occurrence of each symbol. You can generate a set of codes to represent the symbols that will minimize the average bits per code, and no code will be a prefix to any other code.

The JPEG header gives the number of codes of each length (the bit table) and the set of symbols (The value table), to be represented, in ascending code length order, for both AC & DC coefficients, for each color component. To generate the codes start with zero & a code length of the first entry in the bit table. Then increment the code each time. When it is time to change the code length shift the code left the number of times necessary to give the correct length.

Step i: Write the entropy encoded information & binary numbers to the output.

The decompressor reverses the above process.

Entropy Coding:

• 1. Introduction

Entropy Coding is a form of compression that relies on developing "code" words in a library for the input values or "symbols". A very simple implementation of entropy coding would be to describe four kinds of weather by a 2 bit binary code as follows

Symbol	Bit Code
Clear	00
Cloudy	01
Rainy	10
Snowy	11

This would allow a coding algorithm to describe the weather with two bits of information per sample. This is a "fixed length" code. Fixed length codes are best applicable to applications where each of the symbols are equally likely, that is to say where each of the weather types is 25% likely in the above example.

In most real world applications this is not the case, each of the symbols actually have different probabilities of occurring. This leads to the use of "variable length" codes. If an event is most likely to happen more often than the other events, then it makes sense to use a code word that is actually shorter, or requires less information, than the other event codes.

Using the weather example again, say that each event has a probability as follows, we can generate variable length codes

Symbol	% Prob	Bit Code
Clear	50	0
Cloudy	25	10
Rainy	12.5	110
Snowy	12.5	111

Now we can determine the average bit length for a code per symbol.As can be seen, an average of 1.75 bit/symbol is more efficient then the 2 bits/symbol that the fixed length code produced. The codes produced for this example are found using Huffman coding, which is one of the two options that the JPEG standard allows for. The other is known as Arithmetic Coding. This project uses Huffman Coding for the following reasons

• 1. Huffman Coding is simpler.
• 2. Arithmetic Coding is patented and hence has restrictions on its use.

Unfortunately Arithmetic Coding is superior to Huffman Coding in terms of speed and efficiency. However using a patented technology is beyond the scope of this project. Arithmetic Coding partly gains its superiority by being "adaptive", ie being able to produce probability estimates on the fly. Huffman coding on the other hand requires a set of constant probabilities for each of the symbols prior to encryption.

Huffman Coding

Huffman codes are generally derived use a coding "tree" structure. This tree is built by a sequence of pairing operations in which the two least probable symbols are joined at a node. This continues with each node having their probabilities combined and then paired with the next smallest probable symbol until all the symbols represented in the tree structure.

Creating a code from this tree structure is done by assigning a 0 or a 1 bit to each branch of the tree. The code for each symbol is then read by concatenating each bit from the branches, starting at the centre of the structure and extending to the branch for which the relevant symbol is defined.Following this procedure gives a unique code for each symbol of optimal data size.

Note that even though the codes can have different lengths, one code can never be mistaken for another if read from the most significant bit to the least significant bit. This becomes important in JPEG encoding as bit codes are appended to each other without regard for the length of the code.