Decade Counters

The binary counters previously introduced have two to the power n states. But counters with states less than this number are also possible. They are designed to have the number of states in their sequences, which are called truncated sequences. These sequences are achieved by forcing the counter to recycle before going through all of its normal states.

A common modulus for counters with truncated sequences is ten. A counter with ten states in its sequence is called a decade counter. The circuit below is an implementation of a decade counter.

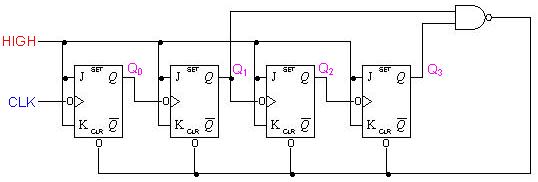
Once the counter counts to ten (1010), all the flip-flops are being cleared. Notice that only Q1 and Q3 are used to decode the count of ten. This is called partial decoding, as none of the other states (zero to nine) have both Q1 and Q3 HIGH at the same time.

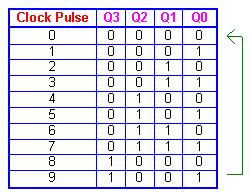
The sequence of the decade counter is shown in the table below

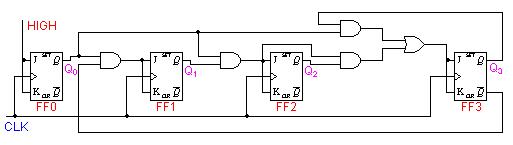
Similar to an asynchronous decade counter, a synchronous decade counter counts from 0 to 9 and then recycles to 0 again. This is done by forcing the 1010 state back to the 0000 state. This so called truncated sequence can be constructed by the following circuit.

From the sequence on the left, we notice that:
Q0 toggles on each clock pulse.
Q1 changes on the next clock pulse each time Q0=1 and Q3=0.
Q2 changes on the next clock pulse each time Q0=Q1=1.
Q3 changes on the next clock pulse each time Q0=1, Q1=1 and Q2=1 (count 7), or when Q0=1 and Q3=1 (count 9).

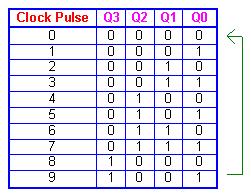
These characteristics are implemented with the AND/OR logic connected as shown in the logic diagram above.