Theoretical Paper
- Computer Organization
- Data Structure
- Digital Electronics
- Object Oriented Programming
- Discrete Mathematics
- Graph Theory
- Operating Systems
- Software Engineering
- Computer Graphics
- Database Management System
- Operation Research
- Computer Networking
- Image Processing
- Internet Technologies
- Micro Processor
- E-Commerce & ERP
Practical Paper
Industrial Training
BCD ADDER
BCD is a class of encoding in which each decimal digit is represented by some fixed number of bits .Usually 4 or 8 bits are used .
| Decimal | BCD |
| 0 | 0000 |
| 1 | 0001 |
| 2 | 0010 |
| 3 | 0011 |
| 4 | 0100 |
| 5 | 0101 |
| 6 | 0110 |
| 7 | 0111 |
| 8 | 1000 |
| 9 | 1001 |
up to 9 the bcd representation is same as the decimal representation and after the 9 <
| Decimal | BCD |
| 10 | 0001 0000 |
| 11 | 0001 0001 |
| 12 | 0001 0010 |
| 13 | 0001 0011 |
| 14 | 0001 0100 |
| 15 | 0001 0101 |
| 16 | 0001 0110 |
| 17 | 0001 1000 |
| 18 | 0001 1000 |
| 19 | 0001 1001 |
the first 4 digits in BCD representation is used to show the first digit in decimal and next four digits in BCD are used to represent next digit in decimal .
TRUTH TABLE
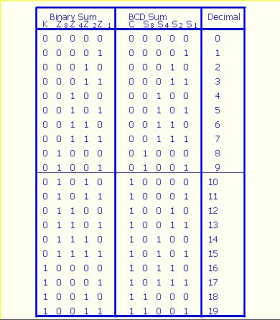
WHY only 4 BIT ADDER CAN NOT BE USED ?
when we provide two 4 bits BCD number to the 4 bit adders , the output exceeds the BCD range , or called BCD representation . WE WANT TO OUTPUT ALSO IN BCD . but when we directly take the output of the 4 bit adder then it will be a invalid representation .
Therefore we need some mechanism through which we can change the output of the 4 bit adder into a valid BCD representation .
if you carry fully see , that the up to when the sum is 9 , the BCD representation is same as the binary representation .
when the sum exceed the 9 , the following condition occur :-
1) either the carry bit is 1
2) the sum is 1010.
3) or the sum is 1100.
for the numbers which does not satisfy the condition of BCD , 6 is added . see in the table , when the sum is 01010 the bcd representation is obtained by adding 6 ., so the representation in BCD is 1 0000.
the condition when 6 is to be added is
F = CO + Z3 Z2 + Z3 Z1
this can be easily obtained by K - map .
where CO is the output carry . and the z3 is the 4 bit , z2 the bit 3 and similarly z1 bit 2

