Relational AlgebraPart-2

In the previous chapter, we introduced relational algebra as a fundamental model of relational database manipulation. In particular, we defined and discussed three important operations it provides: Select, Project and Natural Join. These constitute what is called the basic set of operators and all relational DBMS, without exception, support them. We have presented examples of the power of these operations to construct solutions (derived relations) to various queries. However, there are classes of practical queries for which the basic set is insufficient. This is best illustrated with an example. Using again the same example domain of customers and products they purchase, let us consider the following requirement: "Get the names of customers who had purchased both product number 1 and product number 2"

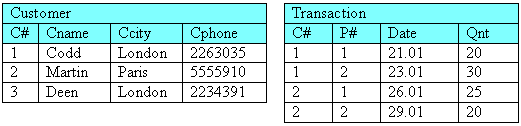
All the required pieces of data are in the relations shown above. It is quite easy to see what the answer is - from the Transaction relation, customers number 1 and number 2 are the ones we are interested in, and cross-referencing the Customer relation (to retrieve their names) the customers are Codd and Martin respectively. Now, how can we construct this solution using the basic operation set? Working backwards, the final relation we wish to construct is a single-column relation with the attribute 'Cname'. Thus, the last operation needed will be a projection of some relation over that attribute. Such a relation must first be the result of joining Customer and Transaction (over 'C#'), since Customer alone does not have data on products purchased. Second, it must contain only tuples of customers who had purchased products 1 and 2, ie. some form of selection must be applied. This analysis suggests that the required sequence of operations is a Join, followed by a Select, and finally a Project.

The following then may be a possible solution:

join Customer AND Transaction over C# giving A

select A where P# = 1 AND P# = 2 giving B

project B over Cname giving Result

The join results in

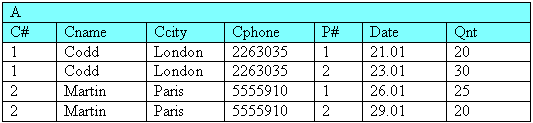
At this point, however, we discover a problem: the selection on A results in an empty relation! The problem is the selection condition: no tuple can possibly satisfy a condition that requires a single attribute to have two different values ("P# = 1 AND P# = 2"). This is obvious once it is pointed out, although it might not have been so at first glance. Thus while the selection statement is syntactically correct, its logic is erroneous. What is needed, effectively, is to select tuples of a particular customer only if there exists one with P# = 1 and another with P# = 2, ie. the form of selection needed is dependent across tuples. But the basic Select operator cannot express this because it operates on each tuple in turn and independently of one another. Thus the proposed solution above is not a solution at all. In fact, no combination of the basic operations can handle the query or other queries of this sort, for example:

"Get the names of customers who bought the product CPU but not the product VDU", or

"Get the names of customers who bought every product type that the company sells", etc.

These examples suggest that additional operations are needed. In the following, we shall present them and show how they are used. Some readers may have noted that if OR was used instead of AND in the selection operation, the desired result would be constructed. However, this is coincidental. The use of OR is logically erroneous-it means one or the other, but not necessarily both. To see this, change the example slightly by deleting the last tuple in Transaction and recompute the result (using OR). Your answer would still be Codd and Martin, but the correct answer should be Codd alone!

We will round up this chapter and our discussion of relational algebra with a discussion of two other important topics: how operations handle "null" values, and how sequences of operations can be optimised for performance.

A null value is inserted into a tuple field to denote an (as yet) unknown value. Clearly, this affects the evaluation of conditions involving attribute values. Exactly how will be explained in Section 6.4. Finally, we will see that there may be several different sequences of operations that derive the same result. In such cases, we may well ask which sequence is more efficient, ie. least costly or better in performance, in some sense. A more precise notion of 'efficiency' of operators and how a given operator sequence can be made more efficient will be discussed in section

Division

As the name of this operation implies, it involves dividing one relation by another. Division is in principle a partitioning operation. Thus, 6 ÷ 2 can be paraphrased as partitioning a single group of 6 into a number of groups of 2 - in this case, 3 groups of 2. The basic terminology used in arithmetic will be used here as well. Thus in an expression like x ÷ y, x is the dividend and y the divisor. Division does not always yield whole groups of the divisor, eg. 7 ÷ 2 gives 3 groups of 2 and a remainder group of 1. Relational division too can leave remainders but, much like integer division, we ignore remainders and focus only on constructing whole groups of the divisor. The manner in which a relational dividend is partitioned is a little more complex. First though, we should ask what aspect of a relation is being partitioned? The answer simply is the set of tuples in the relation. Next, we ask how we decide to group some tuples together and not others? Not surprisingly, the basis for such decisions has to do with the attribute values in the tuples. Let's take a look at an example first before we describe the process more precisely.

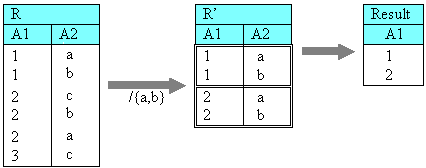
The illustration above shows how we may divide a relation R, which is a simple binary relation in this case with two attributes A1 and A2. For clarity, the values of attribute A1 have been sorted so that a given value appears in contiguous rows (where there's more than one). The question we're interested in is which of these values have in common an arbitrary subset of values of attribute A2. For example,

"which values of A1 share the subset {a,b} of A2?"

By inspecting R, the reader can verify that the answer are the values 1 and 2, because only tuples with these A1values have corresponding A2 entries of both 'a' and 'b'. Put another way, the tuples of R are grouped by the common denominator or divisor {a,b}. This is shown in the relation R' where we emphasise the groups formed using double-line borders. Other tuples (the remainder of the division) are ignored. Note that R' is not the final result of division - it is only an intermediate working result. The desired result are the values of attribute A1 in it, or put another way, the projection of R' over A1.

From this example, we can see that a division of a relation R is performed over some attribute of R. The divisor is a subset of values from that attribute domain and the result is a relation comprising the remaining attributes of R. In relational algebra expessions, the divisor is in fact specified by another relation D. For this to be meaningful at all, D must have at least one attribute in common with the R. The division is over the common attribute(s) and the set of values used as the actual divisor are the values found in D. The general operation is depicted in the figure below.

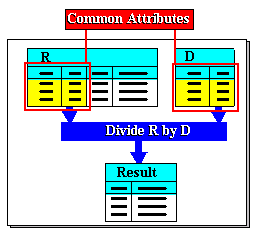
The division operation Figure 6-2 shows a simple example of dividing a binary relation R1 by a unary relation R2. The division is over the shared attribute I2. The divisor is the set {1,2,3}, these being the values found in the shared attribute in R2. Inspecting the tuples of R1, the value 'a' occur in tuples such that their I2 values match the divisor. So 'a' is included in the result. 'b' is not, however, as there is no tuple .

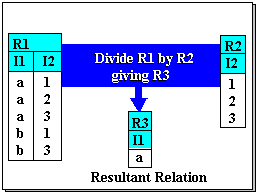
Division of a binary relation by a unary relation

We can now specify the form of the operation:

divide by

giving

and must be names of defined relations or results of previous operations. must be a unique name used to denote the result relation. As mentioned above, the divisor must share attributes with the dividend. In fact, we shall insist (on a stronger condition) that the intension of the divisor must be a subset of the dividend's. This is not really a restriction as any relation that shares attributes with the dividend can be turned into the required form simply by projecting over them.

We can now show how division can be used for the type of queries mentioned in the introduction. Take the query: "Get the names of customers who bought every product type that the company sells"

The Transaction relation records customers who have ever bought anything. For this query, however, we are not interested in the dates or purchase quantities but only in the product types a customer purchased. So we project Transaction over C# and P# to give us a working relation A. This is shown on the left side of the following illustration. Next, we need all the product types the company sells, and these may be obtained by projecting the relation Product over P# to give us a working relation B. This is shown on the right side of the illustration. Formal Definition
To formally define the Divide operation, we will use the notation introduced and used in Chapter 5. However, for convenience, we repeat here principal definitions to be used.

If s denotes a relation, then let

S(s) denote the finite set of attribute names of s (ie. its intension)

T(s) denote the finite set of tuples of s (ie. its extension)

t· a, where t Î T(s) and a Î S(s), denote the value of attribute a in tuple t

Stuple(x) denote the set of elements in tuple x