Normalisation

Suppose we are now given the task of designing and creating a database. How do we produce a good design? What relations should we have in the database? What attributes should these relations have? Good database design needless to say, is important. Careless design can lead to uncontrolled data redundancies that will lead to problems with data anomalies. In this chapter we will examine a process known as Normalisation - a rigorous design tool that is based on the mathematical theory of relations which will result in very practical operational implementations. A properly normalised set of relations actually simplifies the retrieval and maintenance processes and the effort spent in ensuring good structures is certainly a worthwhile investment. Furthermore, if database relations were simply seen as file structures of some vague file system, then the power and flexibility of RDBMS cannot be exploited to the full.

For us to appreciate good design, let us begin by examining some bad ones.

A Bad Design E.Codd has identified certain structural features in a relation which create retrieval and update problems. Suppose we start off with a relation with a structure and details like:

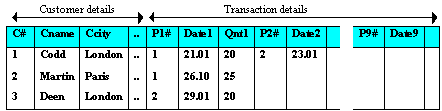
Simple structure
This is a simple and straightforward design. It consists of one relation where we have a single tuple for every customer and under that customer we keep all his transaction records about parts, up to a possible maximum of 9 transactions. For every new transaction, we need not repeat the customer details (of name, city and telephone), we simply add on a transaction detail. However, we note the following disadvantages:

The relation is wide and clumsy

We have set a limit of 9 (or whatever reasonable value) transactions per customer. What if a customer has more than 9 transactions? For customers with less than 9 transactions, it appears that we have to store null values in the remaining spaces. What a waste of space! The transactions appear to be kept in ascending order of P#s. What if we have to delete, for customer Codd, the part numbered 1- should we move the part numbered 2 up (or rather, left)? If we did, what if we decide later to re-insert part 2? The additions and deletions can cause awkward data shuffling.

Let us try to construct a query to "Find which customer(s) bought P# 2" ? The query would have to access every customer tuple and for each tuple, examine every of its transaction looking for

(P1# = 2) OR (P2# = 2) OR (P3# = 2) ... OR (P9# = 2)

A comparatively simple query seems to require a clumsy retrieval formulation!

Another Bad Design
Alternatively, why don't we re-structure our relation such that we do not restrict the number of transactions per customer. We can do this with the following structure:

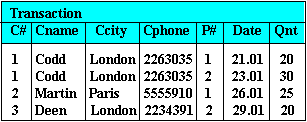
This way, a customer can have just any number of Part transactions without worrying about any upper limit or wasted space through null values (as it was with the previous structure).

Constructing a query to "Find which customer(s) bought P# 2" is not as cumbersome as before as one can now simply state: P# = 2. But again, this structure is not without its faults:

1.It seems a waste of storage to keep repeated values of Cname, Ccity and Cphone.
2. If C# 1 were to change his telephone number, we would have to ensure that we update ALL occurrences of C# 1's Cphone values. This means updating tuple 1, tuple 2 and all other tuples where there is an occurrence of C# 1. Otherwise, our database would be left in an inconsistent state.
3.Suppose we now have a new customer with C# 4. However, there is no part transaction yet with the customer as he has not ordered anything yet.

We may find that we cannot insert this new information because we do not have a P# which serves as part of the 'primary key' of a tuple. (A primary key cannot have null values).

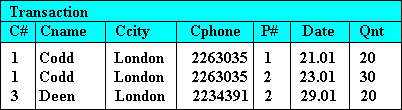
But then, suppose we need information about the customer "Martin", say the city he is located in. Unfortunately as information about Martin was held in only that tuple and having the entire tuple deleted because of its P# transaction, meant also that we have lost all information about Martin from the relation. As illustrated in the above instances, we note that badly designed, unnormalised relations waste storage space. Worse, they give rise to the following storage irregularities:

1. Update anomaly: Data inconsistency or loss of data integrity can arise from data redundancy/repetition and partial update.
2. Insertion anomaly: Data cannot be added because some other data is absent.
3. Deletion anomaly: Data maybe unintentionally lost through the deletion of other data.


The Need for Normalisation
Intuitively, it would seem that these undesirable features can be removed by breaking a relation into other relations with desirable structures. We shall attempt by splitting the above Transaction relation into the following two relations, Customer and Transaction, which can be viewed as entities with a one to many relationship.

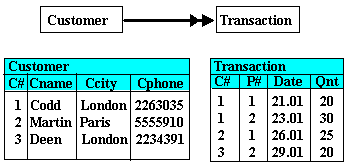
M data relationships

Let us see if this new design will alleviate the above storage anomalies:

Update anomaly

If C# 1 were to change his telephone number, as there is only one occurrence of the tuple in the Customer relation, we need to update only that one tuple as there are no redundant/duplicate tuples.

Addition anomaly

Adding a new customer with C# 4 can be easily done in the Customer relation of which C# serves as the primary key. With no P# yet, a tuple in Transaction need not be created.

Deletion anomaly

Canceling the third transaction about 25 of P# 1 being ordered on 26 Jan would now mean deleting only the third tuple of the new Transaction relation above. This leaves information about Martin still intact in the new Customer relation.

This process of reducing a relation into simpler structures is the process of Normalisation.

Normalisation may be defined as a step by step reversible process of transforming an unnormalised relation into relations with progressively simpler structures. Since the process is reversible, no information is lost in the transformation.

Normalisation removes (or more accurately, minimises) the undesirable properties by working through a series of stages called Normal Forms. Originally, Codd defined three types of undesirable properties:

1. Data aggregates
2. Partial key dependency
3. Indirect key dependency

and the three stages of normalisation that remove the associated problems are known, respectively, as the:

1. First Normal Form (1NF)
2. Second Normal Form (2NF), and
3. Third Normal Form (3NF)

We shall now show a more formal process on how we can decompose relations into multiple relations by using the Normal Form rules for structuring.

First Normal Form (1NF) The purpose of the First Normal Form (1NF) is to simplify the structure of a relation by ensuring that it does not contain data aggregates or repeating groups. By this we mean that no attribute value can have a set of values. In the example below, any one customer has a group of several telephone entries:

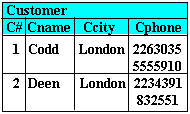
Presence of repeating groups This is thus not in 1NF. It must be "flattened". This can be achieved by ensuring that every tuple defines a single entity by containing only atomic values. One can either re-organise into one relation as in:

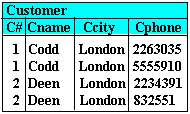
Atomic values in tuples or split into multiple relations as in: