Walsh transform

The system of Walsh functions (or, simply, Walsh system) may be viewed as a discrete, digital counterpart of continuous, analog system of trigonometric functions on the unit interval. Unlike trigonometric functions, Walsh functions are only piecewise-continuous, and, in fact, are piecewise constant. The functions take the values -1 and +1 only, on sub-intervals defined by dyadic fractions.

Both systems form a complete, orthonomal set of functions, an orthonormal basis in Hilbert space L^2[0,1] of the square-integrable functions on the unit interval. Both are systems of bounded functions, unlike, say, Haar system or Franklin system.

Both trigonometric and Walsh systems admit natural extension by periodicity from the unit interval to the real line \mathbb R . Furthermore, both Fourier analysis on the unit interval (Fourier series) and on the real line (Fourier transform) have their digital counterparts defined via Walsh system, the Walsh series analogous to the Fourier series, and the Hadamard transform analogous to the Fourier Transform.

Walsh functions, series, and transforms find various applications in physics and engineering, especially in digital signal processing. They are used in speech recognition, in medical and biological image processing, in digital holography, and other areas.

Historically, various numerations of Walsh functions have been used, none of which could be considered particularly superior to another. In what follows, we will use so called Walsh-Paley numeration.

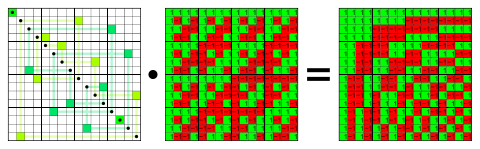
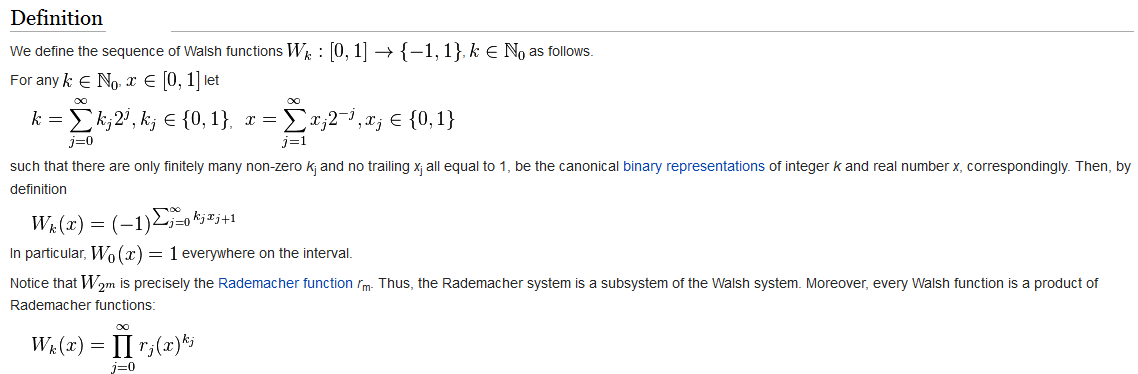
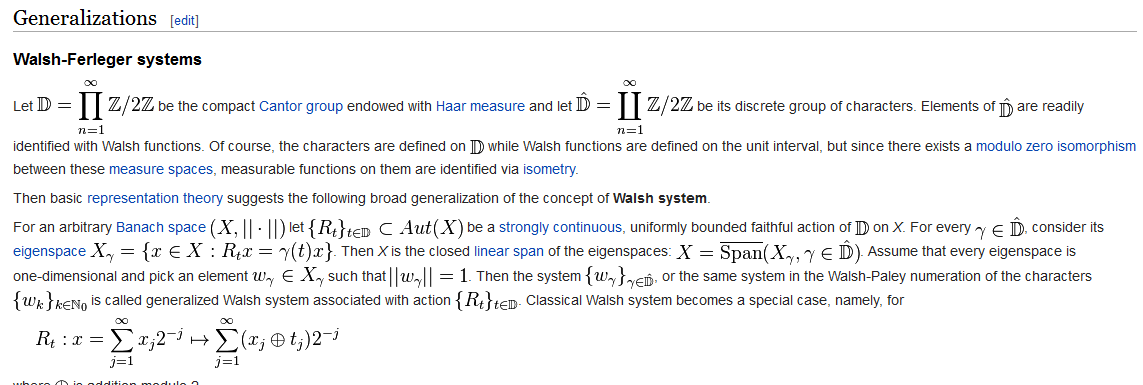
In early nineties, Serge Ferleger and Fyodor Sukochev have shown that in a broad class of Banach spaces (so called UMD spaces [1]) generalized Walsh systems have many properties similar to the classical one: they form a Schauder basis [2] and a uniform finite dimensional decomposition [3] in the space, have property of random unconditional convergence.[4] One important example of generalized Walsh system is Fermion Walsh system in non-commutative Lp spaces associated with hyperfinite type II factor.

Fermion Walsh system
Fermion Walsh system is a non-commutative, or "quantum" analogue of the classical Walsh system. Unlike the latter, it consists of operators, not functions. Nevertheless, both systems share many important properties, e.g., both form an orthonormal basis in corresponding Hilbert space, or Schauder basis in corresponding symmetric spaces. Elements of the Fermion Walsh system will be called Walsh operators.

The word "Fermion" in the name of the system is explained by the fact that the enveloping operator space, so called hyperfinite type II factor \mathcal R may be viewed as the space of observables of the system of countably infinite number of distinct spin \frac{1}{2} fermions. Each Rademacher operator acts on one particular fermion coordinate only, and there it is a Pauli matrix. It may be identified with observable measuring spin component of that fermion along one of the axes \{x,y,z\} in spin space. Thus, Walsh operator is measuring spin of a subset of the fermions, each along its own axis.

Precise construction is as follows.