DCT

The discrete cosine transform (DCT) helps separate the image into parts (or spectral sub-bands) of differing importance (with respect to the image's visual quality). The DCT is similar to the discrete Fourier transform: it transforms a signal or image from the spatial domain to the frequency domain

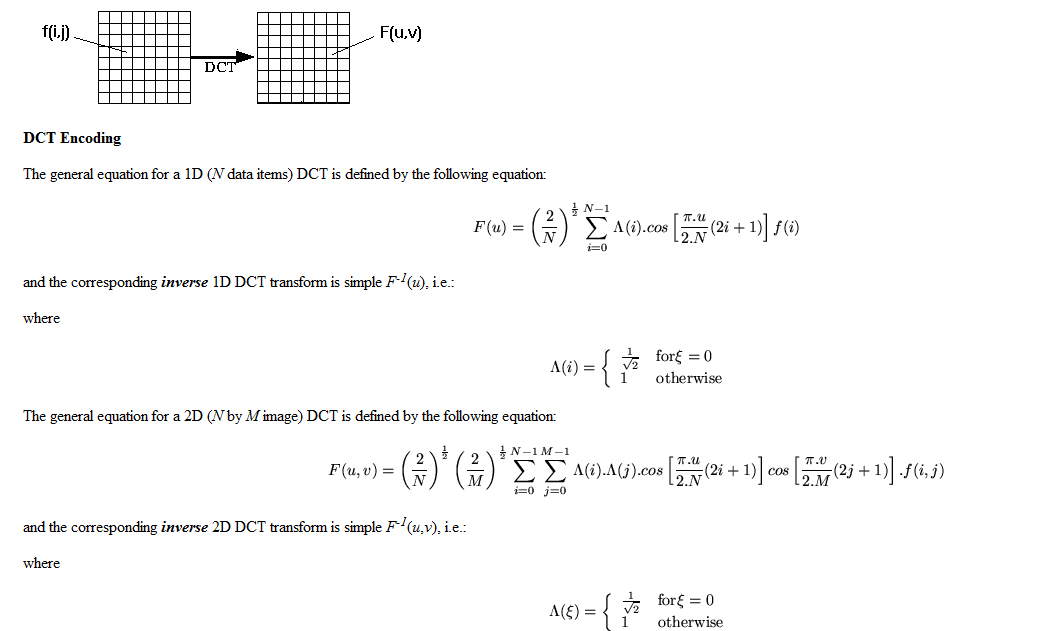
the basic operation of the dct is as follows:

• the input image is n by m;
• f(i,j) is the intensity of the pixel in row i and column j;
• f(u,v) is the dct coefficient in row k1 and column k2 of the dct matrix.
• for most images, much of the signal energy lies at low frequencies; these appear in the upper left corner of the dct.
• compression is achieved since the lower right values represent higher frequencies, and are often small - small enough to be neglected with little visible distortion.
• the dct input is an 8 by 8 array of integers. this array contains each pixel's gray scale level;
• 8 bit pixels have levels from 0 to 255.

• therefore an 8 point dct would be:

  where

  
  
  

  question: what is f[0,0]?

  answer: they define dc and ac components.

• the output array of dct coefficients contains integers; these can range from -1024 to 1023.

• it is computationally easier to implement and more efficient to regard the dct as a set of basis functions which given a known input array size (8 x 8) can be precomputed and stored. this involves simply computing values for a convolution mask (8 x8 window) that get applied (summ values x pixelthe window overlap with image apply window accros all rows/columns of image). the values as simply calculated from the dct formula. the 64 (8 x 8) dct basis functions are illustrated in.
  
  
  
  

  Why DCT not FFT?
  DCT is similar to the Fast Fourier Transform (FFT), but can approximate lines well with fewer coefficients

  
  
  
  
  

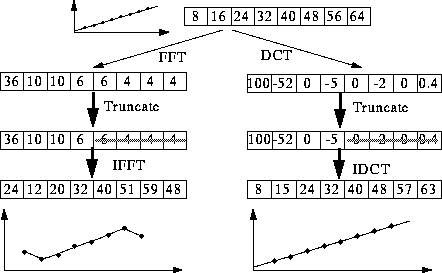
  DCT/FFT Comparison
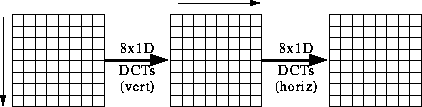
  Computing the 2D DCT
  Factoring reduces problem to a series of 1D DCTs.
  1. apply 1D DCT (Vertically) to Columns
  2. apply 1D DCT (Horizontally) to resultant Vertical DCT above.
  3. or alternatively Horizontal to Vertical.

  
  
  
  
  

  Most software implementations use fixed point arithmetic. Some fast implementations approximate coefficients so all multiplies are shifts and adds.
  
  World record is 11 multiplies and 29 adds. (C. Loeffler, A. Ligtenberg and G. Moschytz, "Practical Fast 1-D DCT Algorithms with 11 Multiplications", Proc. Int'l. Conf. on Acoustics, Speech, and Signal Processing 1989 (ICASSP `89), pp. 988-991)

  
  
  
  Previous
  Next