mcatutorials.com | Data Representation

Data Representation refers to the methods used internally to represent information stored in a computer. Computers store lots of different types of information:

numbers
text
graphics of many varieties (stills, video, animation)
sound

At least, these all seem different to us. However, ALL types of information stored in a computer are stored internally in the same simple format: a sequence of 0's and 1's. How can a sequence of 0's and 1's represent things as diverse as your photograph, your favorite song, a recent movie, and your term paper?

It all depends on how we interpret the information. Computers use numeric codes to represent all the information they store. These codes are similar to those you may have used as a child to encrypt secret notes: let 1 stand for A, 2 stand for B, etc. With this code, any written message can be represented numerically. The codes used by computers are a bit more sophisticated, and they are based on the binary number system (base two) instead of the more familiar (for the moment, at least!) decimal system. Computers use a variety of different codes. Some are used for numbers, others for text, and still others for sound and graphics.

Memory Structure in Computer

Memory consists of bits (0 or 1)
- a single bit can represent two pieces of information
bytes (=8 bits)
- a single byte can represent 256 = 2x2x2x2x2x2x2x2 = 2⁸ pieces of information
words (=2,4, or 8 bytes)
- a 2 byte word can represent 256² pieces of information (approximately 65 thousand).
Byte addressable - each byte has its own address.

Binary Numbers

Normally we write numbers using digits 0 to 9. This is called base 10. However, any positive integer (whole number) can be easily represented by a sequence of 0's and 1's. Numbers in this form are said to be in base 2 and they are called binary numbers. Base 10 numbers use a positional system based on powers of 10 to indicate their value. The number 123 is really 1 hundred + 2 tens + 3 ones. The value of each position is determined by ever-higher powers of 10, read from left to right. Base 2 works the same way, just with different powers. The number 101 in base 2 is really 1 four + 0 twos + 1 one (which equals 5 in base 10). For more of a comparison

Text

Text can be represented easily by assigning a unique numeric value for each symbol used in the text. For example, the widely used ASCII code (American Standard Code for Information Interchange) defines 128 different symbols (all the characters found on a standard keyboard, plus a few extra), and assigns to each a unique numeric code between 0 and 127. In ASCII, an "A" is 65," B" is 66, "a" is 97, "b" is 98, and so forth. When you save a file as "plain text", it is stored using ASCII. ASCII format uses 1 byte per character 1 byte gives only 256 (128 standard and 128 non-standard) possible characters The code value for any character can be converted to base 2, so any written message made up of ASCII characters can be converted to a string of 0's and 1's.

Graphics

Graphics that are displayed on a computer screen consist of pixels: the tiny "dots" of color that collectively "paint" a graphic image on a computer screen. The pixels are organized into many rows on the screen. In one common configuration, each row is 640 pixels long, and there are 480 such rows. Another configuration (and the one used on the screens in the lab) is 800 pixels per row with 600 rows, which is referred to as a "resolution of 800x600." Each pixel has two properties: its location on the screen and its color.

A graphic image can be represented by a list of pixels. Imagine all the rows of pixels on the screen laid out end to end in one long row. This gives the pixel list, and a pixel's location in the list corresponds to its position on the screen. A pixel's color is represented by a binary code, and consists of a certain number of bits. In a monochrome (black and white) image, only 1 bit is needed per pixel: 0 for black, 1 for white, for example. A 16 color image requires 4 bits per pixel. Modern display hardware allows for 24 bits per pixel, which provides an astounding array of 16.7 million possible colors for each pixel!

Compression

Files today are so information-rich that they have become very large. This is particularly true of graphics files. With so many pixels in the list, and so many bits per pixel, a graphic file can easily take up over a megabyte of storage. Files containing large software applications can require 50 megabytes or more! This causes two problems: it becomes costly to store the files (requires many floppy disks or excessive room on a hard drive), and it becomes costly to transmit these files over networks and phone lines because the transmission takes a long time. In addition to studying how various types of data are represented, you will have the opportunity today to look at a technique known as data compression. The basic idea of compression is to make a file shorter by removing redundancies (repeated patterns of bits) from it. This shortened file must of course be de-compressed - have its redundancies put back in - in order to be used. However, it can be stored or transmitted in its shorter compressed form, saving both time and money.

Number System defines a set of values used to represent ‘quantity’.

Base or Radix: The total number of digits available in a number system .
Decimal Number System:

There are 10 digits i.e 1, 2, 3, 4, 5, 6, 7, 8, 9 available in decimal number system. It is known as Base 10 system. The value of a digit in a number depends upon its position in the number e.g. the number 546 in this system is represented as (546)₁₀

546 = (4*10²) + (8*10¹) + (6*10⁰)

Binary Number System
The Binary Number System contains 2 unique digits 0 and 1. it is known as Base 2 system.
Octal Number System
There are 8 unique digits available in octal number system. These are 0, 1, 2, 3, 4, 5, 6, 7. thus, any number formed is the combination of these digits. It is known as Base 8 system.
Hexadecimal Number System
There are 16 unique digits available in Hexadecimal number system. These are 0, 1, 2, 3, 4, 5, 6, 7, 8, A, B, C, D, E, F where A denotes 10, B denotes 11………,F denotes 15. thus any number formed is a combination of these digits. It is known as Base 16 system.

Converting Between Number Bases

Converting Decimal to Binary, Octal and Hexadecimal
Integer Part
Remainder method

Divide the decimal number by the base of the target number system that is, to convert decimal to binary, divide the decimal number with 2 (the base of binary number system), 8 for octal and 16 for hexadecimal.
Note the remainder separately as the first digit from the right. In case of hexadecimal , if the remainder exceeds 9, convert the remainder into equivalent hexadecimal form. For e.g., if the remainder is 10 then note the remainder as A.
Continually repeat the process of dividing until the quotient is zero and keep writing the remainders after each step of division.
Finally, when no more division can occur, write down the remainders in reverse order.

Fractional Part

Multiply the fractional part by the value of the new base.
Record the integer part if it exits, else record 0.
Repeat step 1 with the result of the previous multiplication and then step 2, until the fractional part becomes 0. in case of infinite calculations, generally 6 digits are taken.

Converting Binary, Octal and Hexadecimal to Decimal
The method used for conversion of a binary, octal and hexadecimal number to decimal number involves each digit of the binary, octal or hexadecimal number to be multiplied by its weighted position, and then each of the weighted values are added to get the decimal number.

Example:

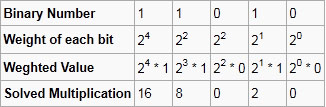
Sum of weight of all bits = 16 + 8 +0 + 2 + 0 = 26
Thus, the decimal equivalent of (11010)₂ is (26)₁₀

Converting Between Octal and Hexadecimal
Steps of conversion

Convert each octal digit to 3-bit binary form
Combine all the 3-bit binary numbers.
Segregate the binary numbers into 4-bit binary form by starting the first number from the right bit (LSB) towards the number on the left bit (MSB).
Finally, convert these 4-bit blocks into their respective hexadecimal symbols.

Enroll now!

Theoretical Paper

Practical Paper

Industrial Training

Data Representation