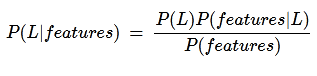Classification Algorithms - Naïve Bayes

Introduction to Naïve Bayes Algorithm

Naïve Bayes algorithms is a classification technique based on applying Bayes’ theorem with a strong assumption that all the predictors are independent to each other. In simple words, the assumption is that the presence of a feature in a class is independent to the presence of any other feature in the same class. For example, a phone may be considered as smart if it is having touch screen, internet facility, good camera etc. Though all these features are dependent on each other, they contribute independently to the probability of that the phone is a smart phone.

In Bayesian classification, the main interest is to find the posterior probabilities i.e. the probability of a label given some observed features, 𝑃(𝐿 | 𝑓𝑒𝑎𝑡𝑢𝑟𝑒𝑠). With the help of Bayes theorem, we can express this in quantitative form as follows −

Here, (𝐿 | 𝑓𝑒𝑎𝑡𝑢𝑟𝑒𝑠) is the posterior probability of class.

𝑃(𝐿) is the prior probability of class.

𝑃(𝑓𝑒𝑎𝑡𝑢𝑟𝑒𝑠|𝐿) is the likelihood which is the probability of predictor given class.

𝑃(𝑓𝑒𝑎𝑡𝑢𝑟𝑒𝑠) is the prior probability of predictor.

Building model using Naïve Bayes in Python

Python library, Scikit learn is the most useful library that helps us to build a Naïve Bayes model in Python. We have the following three types of Naïve Bayes model under Scikit learn Python library −

Gaussian Naïve Bayes

It is the simplest Naïve Bayes classifier having the assumption that the data from each label is drawn from a simple Gaussian distribution.

Multinomial Naïve Bayes

Another useful Naïve Bayes classifier is Multinomial Naïve Bayes in which the features are assumed to be drawn from a simple Multinomial distribution. Such kind of Naïve Bayes are most appropriate for the features that represents discrete counts.

Bernoulli Naïve Bayes

Another important model is Bernoulli Naïve Bayes in which features are assumed to be binary (0s and 1s). Text classification with ‘bag of words’ model can be an application of Bernoulli Naïve Bayes.