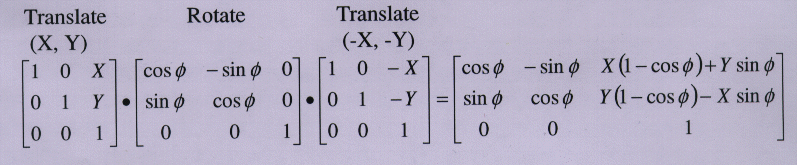Theoretical Paper
- Computer Organization
- Data Structure
- Digital Electronics
- Object Oriented Programming
- Discrete Mathematics
- Graph Theory
- Operating Systems
- Software Engineering
- Computer Graphics
- Database Management System
- Operation Research
- Computer Networking
- Image Processing
- Internet Technologies
- Micro Processor
- E-Commerce & ERP
Practical Paper
Industrial Training
Composite Transformation
1.0 what is a two dimensional transformation?2.0 a matrix representation of two dimensional transformations
3.0 composite transformations
1.0 what is a two dimensional transformation?
a two dimensional transformation is any operation on a point in space (x, y) that maps that point's coordinates into a new set of coordinates
(x1, y1). instead of applying a transformation to every point in every line that makes up an object, the
transformation is applied only to the vertices of the object and then new lines are drawn between the resulting endpoints.
the basic transformations are:
go back to two dimensional transformation teaching tool
1.1 translation
moving an object is called a translation. we translate an object by translating each
vertex in the object.
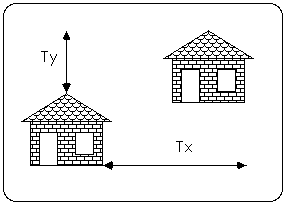
this is accomplished by adding a translation factor tx to the x coordinate and ty to the y coordinate of each vertex.
the transformation equations for translation are:
y' = y + ty
go back to two dimensional transformation teaching tool
1.2 scaling
changing the size of an object is accomplished by a transformation called scaling. scaling an object is implemented by scaling the x and y coordinates of each vertex in
the object.
">
this is accomplished by multiplying the x coordinate by sx, the scale factor of x, and the y coordinate by sy, the scale factor of y.
the transformation equations for scaling are:
y' = y*sy
if the scaling factors are less than one, the object will appear smaller. if the scaling factors are
greater than one, the object will appear larger. if sx = sy = 1, the object is unchanged.
if an object
that is scaled is not positioned at the origin, the scaled figure will also be translated.
this change in position can be compensated for by scaling about an arbitrary point, usually a corner or the center of the object. scaling about an
arbitrary point is discussed in section 2.3.1.
rotation is a transformation that causes a point p to be moved relative to a central point, without changing the distance of
p from that point. this transformation is accomplished by applying the rotation equation to each vertex of the object.
a rotation is specified by providing an angle, b, indicating how many degrees of rotation are desired. this angle may be either positive or negative. a positive angle indicates a counter-clockwise rotation about the origin.
the transformation equations for rotation are:
go back to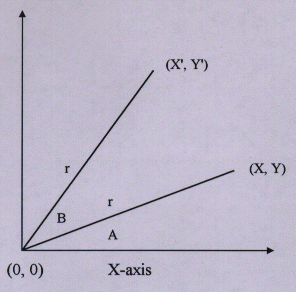
two dimensional transformation teaching tool
1.3 rotation
y' = x sinb + y cosb
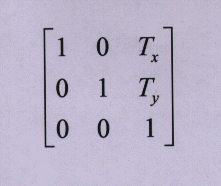
these equations can be easily derived from the figure above, in which a rotation by b transforms p1(x,y) into p2(x',y'). because the rotation is about the origin, the distance from the origin to p1 and p2 labeled r in the figure, are equal.
by simple trigonometry, we find that
y = r * sina
and
cos(a + b) = x'/r
substitution using the double angle formula
cos(a+b) = cosa * cosb - sina * sinb
we see that
y'/r = (y/r) * cosb + (x/r) * sinb
y' = y cosb + x sinb
thus,
y' = x sinb + y cosb
rotation about an arbitrary point is discussed in section 2.3.1.
go back to two dimensional transformation teaching tool
2.0 a matrix representation of two dimensional transformations
although the equations shown above could be used to implement programs to do scaling, rotation and translation, it is more reasonable to find a consistent way to handle all three transformations. this can be done by expressing the points as homogeneous coordinates. then, each of the transformation equations can be represented as three dimensional matrices. matrices provide an efficient method for performing sequences of transformations without calculating intermediate coordinate values.
to use a matrix representation, a two dimensional point is represented in homogeneous coordinates by a triple (x,y,w), instead of (x,y).
triples of coordinates typically represent points in 3-space, but here it is used to represent points in 2-space. usually w is fixed
at 1.
now we can now use 3 x 3 matrices to represent the basic transformation functions. applying a transformation to a point is
accomplished by multiplying the homogenous coordinates of the point by the appropriate transformation matrix.
go back to two dimensional transformation teaching tool
2.1 translation
the matrix for translation is:
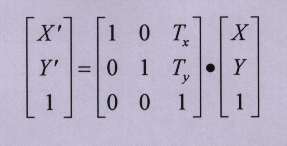
and the equations for the translation transformation become
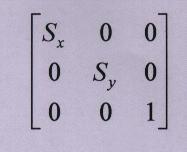
go back to two dimensional transformation teaching tool
2.2 scale
the matrix for scaling is:
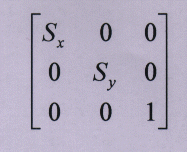
and the equations for the scaling transformation relative to the origin become
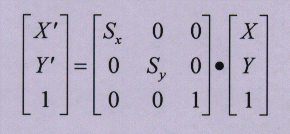
go back to two dimensional transformation teaching tool
2.3 rotation
the matrix for rotation is:
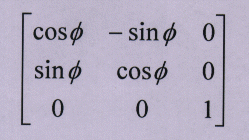
and the equations for the rotation transformation about the origin become
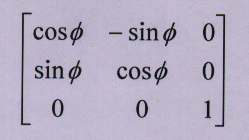
go back to two dimensional transformation teaching tool
3.0 composite transformations
we use matrix composition to produce any series of transformations that are desired. the transformation sequence is then defined by multiplying the transformation matrices together. the order of the multiplication sequence is important. remember matrix multiplication is not commutative.
3.1 rotation or scaling about an arbitrary point
the scaling and rotation transformations are defined about the origin. the user might wish to
rotate or scale about an arbitrary point. this can be done using a combination of
transformations we already know about.
go back to two dimensional transformation teaching tool
1.translate the object by (-x1, -y1)
this series of steps can be performed as following:
2.scale by (sx, sy)
3.translate the object by (x1, y1)
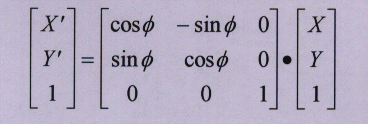
1.translate the object by (-x1, -y1)
the matrix representation of these steps is:
2.rotate (ø)
3.translate the object by (x1, y1)
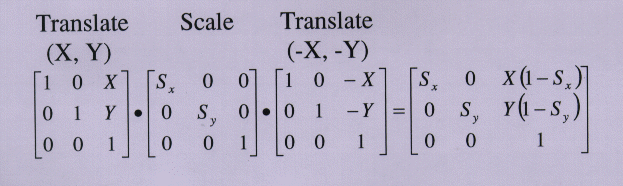
3.2 multiple transformations
sometimes we wish to perform a series of transformations. for example, we might want to rotate by (ø),
translate by (tx, ty) and scale by (sx,sy). the sequence of such a series is:
1.rotate (ø)
the matrix representation of these steps is:
2.translate (tx, ty)
3.scale (sx, sy)
