Theoretical Paper
- Computer Organization
- Data Structure
- Digital Electronics
- Object Oriented Programming
- Discrete Mathematics
- Graph Theory
- Operating Systems
- Software Engineering
- Computer Graphics
- Database Management System
- Operation Research
- Computer Networking
- Image Processing
- Internet Technologies
- Micro Processor
- E-Commerce & ERP
Practical Paper
Industrial Training
Threaded Binary Trees
Threaded Binary Trees
Both the recursive and non-recursive procedures for binary tree traversal require that pointers to all of the free nodes be kept temporarily on a stack. It is possible to write binary tree traversal procedure that do not require that any pointers to the nodes be put on the stack. Such procedures eliminate the overhead (time and memory) involved in initialising, ushing and popping the stack.
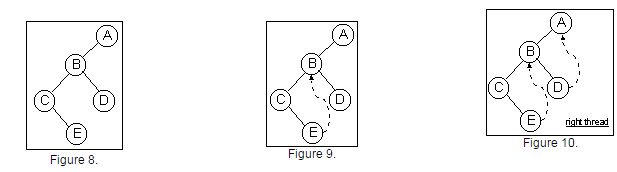
In order to get an idea of how such binary-tree-traversal procedures work, let us look at the tree in Figure 8. First we follow the left pointers until we reach node C , without, however, pushing the pointers to A , B and C onto a stack. For inorder traversal the data for node C is then printed, after which C 's right pointer is followed to node E . Then the data from node E is printed. The next step in our inorder traversal is to go back to node B and print its data; however, we did not save any pointers. But suppose that when we created the tree we had replaced the NULL right pointer in node E with a pointer back to node B . We could then easily follow this pointer back to node B (see Figure 9 ).
Similarly, suppose we replace the normal NULL right pointer of D with a pointer back up to A , as in Figure 10. Then after printing the data in D , we can easily jump up to A and print its data. These pointers which point inorder successor of a node are called right threads . Each right thread replaces a normal right pointer in a tree node. Likewise we can have left threads which point to the inorder predecessor of a node.
The only problem with threads is that the coding requires that we know whether a pointer is a normal pointer to a child or a thread that points back to a inorder successor or inorder predecessor node. One solution to this problem is to add to the data in each tree node two fields which indicate whether the left and right pointers in that node are normal pointers or threads. For example, these fields might be boolean variables, left and right . The variable right is true if the right pointer is a thread and false if it is a normal right pointer. Likewise the variable left is true if the left pointer is a thread and false if it is a normal left pointer. If we add these boolean variables to each tree node, we would make the following structure declaration for a node.
struct thtree
{
enum boolean left ;
struct thtree *leftchild ;
int data ;
struct thtree *rightchild ;
enum boolen right ;
} ;
Thus each node would contain data, a left pointer, a true or false value for left thread, a right pointer and a true or false value for right thread. The program to implement a threaded binary tree is given below. The program also shows how to insert nodes in a threaded binary tree, delete nodes from it and traverse it in inorder traversal.
/* Program to implement threaded binary tree */
#include "alloc.h"
enum boolean
{
false = 0 ,
true = 1 ,
} ;
struct thtree
{
enum boolean left ;
struct thtree *leftchild ;
int data ;
struct thtree *rightchild ;
enum boolen right ;
} ;
main( )
{
struct thtree *th_head ;
th_head = NULL ;/* empty tree */
insert ( &th_head, 11 ) ;
insert ( &th_head, 9 ) ;
insert ( &th_head, 13 ) ;
insert ( &th_head, 8 ) ;
insert ( &th_head, 10 ) ;
insert ( &th_head, 12 ) ;
insert ( &th_head, 14 ) ;
insert ( &th_head, 15 ) ;
insert ( &th_head, 7 ) ;
clrscr( ) ;
printf ( "Threaded binary tree before deletion: " ) ;
inorder ( th_head ) ;
delete ( &th_head, 10 ) ;
printf ( "\nThreaded binary tree after deletion: " ) ;
inorder ( th_head ) ;
delete ( &th_head, 14 ) ;
printf ( "\nThreaded binary tree after deletion: " ) ;
inorder ( th_head ) ;
delete ( &th_head, 8 ) ;
printf ( "\nThreaded binary tree after deletion: " ) ;
inorder ( th_head ) ;
delete ( &th_head, 13 ) ;
printf ( "\nThreaded binary tree after deletion: " ) ;
inorder ( th_head ) ;
}
/* inserts a node in a threaded binary tree */
insert ( struct thtree **s, int num )
{
struct thtree *head = *s , *p, *z ;
/* allocating a new node */
z = malloc ( sizeof ( struct thtree ) ) ;
z -> left = true ; /* indicates a thread */
z -> data = num ; /* assign new data */
z -> right = true ; /* indicates a thread */
/* if tree is empty */
if ( *s == NULL )
{
head = malloc ( sizeof ( struct thtree ) ) ;
/* the entire tree is treated as a left subtree of the head node */
head -> left = false ;
head -> leftchild = z ; /* z becomes leftchild of the head node */
head -> data = -9999 ; /* no data */
head -> rightchild = head ; /* right link will always be pointing to itself */
head -> right = false ;
*s = head ;
z -> leftchild = head ; /* left thread to head */
z -> rightchild = head ; /* right thread to head */
}
else /* if tree is non-empty */
{
p = head -> leftchild ;
/* traverse till the thread is found attached to the head */
while ( p != head )
{
if ( p -> data > num )
{
if ( p -> left != true ) /* checking for a thread */
p = p -> leftchild ;
else
{
z -> leftchild = p -> leftchild ;
p -> leftchild = z ;
p -> left = false ; /* indicates a link */
z -> right = true ;
z -> rightchild = p ;
return ;
}
}
else
{
if ( p -> data < num )
{
if ( p -> right != true )
p = p -> rightchild ;
else
{
z -> rightchild = p -> rightchild ;
p -> rightchild = z ;
p -> right = false ; /* indicates a link */
z -> left = true ;
z -> leftchild = p ;
return ;
}
}
}
}
}
}
/* deletes a node from the binary search tree */
delete ( struct thtree **root, int num )
{
int found ;
struct thtree *parent, *x, *xsucc ;
/* if tree is empty */
if ( *root == NULL )
{
printf ( "\nTree is empty" ) ;
return ;
}
parent = x = NULL ;
/* call to search function to find the node to be deleted */
search ( root, num, &parent, &x, &found ) ;
/* if the node to deleted is not found */
if ( found == false )
{
printf ( "\nData to be deleted, not found" ) ;
return ;
}
/* if the node to be deleted has two children */
if ( x -> left == false && x -> right == false )
{
parent = x ;
xsucc = x -> rightchild ;
while ( xsucc -> left == false )
{
parent = xsucc ;
xsucc = xsucc -> leftchild ;
}
x -> data = xsucc -> data ;
x = xsucc ;
}
/* if the node to be deleted has no child */
if ( x -> left == true && x -> right == true )
{
if ( parent -> rightchild == x )
{
parent -> right = true ;
parent -> rightchild = x -> rightchild ;
}
else
{
parent -> left = true ;
parent -> leftchild = x -> leftchild ;
}
free ( x ) ;
return ;
}
/* if the node to be deleted has only rightchild */
if ( x -> left == true && x -> right == false )
{
if ( parent -> leftchild == x )
{
parent -> leftchild = x -> rightchild ;
x -> rightchild -> leftchild = x -> leftchild ;
}
else
{
parent -> rightchild = x -> rightchild ;
x -> rightchild -> leftchild = parent ;
}
free ( x ) ;
return ;
}
/* if the node to be deleted has only left child */
if ( x -> left == false && x -> right == true )
{
if ( parent -> leftchild == x )
{
parent -> leftchild = x -> leftchild ;
x -> leftchild -> rightchild = parent ;
}
else
{
parent -> rightchild = x -> leftchild ;
x -> leftchild -> rightchild = x -> rightchild ;
}
free ( x ) ;
return ;
}
}
/* returns the address of the node to be deleted, address of its parent and whether the node is found or not */
search ( struct thtree **root, int num, struct thtree **par, struct thtree **x, int *found )
{
struct thtree *q ;
q = ( *root ) -> leftchild ;
*found = false ;
*par = NULL ;
while ( q != root )
{
/* if the node to be deleted is found */
if ( q -> data == num )
{
*found = true ;
*x = q ;
return ;
}
if ( q -> data > num )
{
*par = q ;
q = q -> leftchild ;
}
else
{
*par = q ;
q = q -> rightchild ;
}
}
}
/* traverses the threaded binary tree in inorder */
inorder ( struct thtree *root )
{
struct thtree *p ;
p = root -> leftchild ;
while ( p != root )
{
while ( p -> left == false )
p = p -> leftchild ;
printf ( "%d ", p -> data ) ;
while ( p -> right == true )
{
p = p -> rightchild ;
if ( p == root )
break ;
printf ( "%d ", p -> data ) ;
}
p = p -> rightchild ;
}
}
And now a brief explanation about the program.
We have used an enumerated data type boolean is used to represent, if the thread is present or not. If the left is true there is a left thread means the node has no left child, if the right is true it shows the presence of right thread and the node has no right child. To insert a new node in a threaded tree, the insert( ) function is called which first checks for the empty tree. If the tree is found to be empty a head node is created and the node is joined as its left subtree with both links converted to threads by making left and right both true and leftchild and rightchild pointing back to the head node. Otherwise, the node is inserted into the tree so that a threaded binary search tree is created. Deletion of a node from the threaded binary tree is similar to that of a normal binary tree. That is, we have to identify the four possibilities about the node being deleted:
-
No node in the tree contains the specified data.
-
The node containing the data has no children.
-
The node containing the data has exactly one child.
-
The node containing the data has two children.
The treatment given to these possibilties is same as the one discussed in the previous section on binary trees except that some minor readjustment of threads.
The threaded binary tree's inorder traversal is different than a normal tree in the sense that we do not have to stack the pointers to nodes visited earlier so as to reach them later. This is avoided by using the threads to ancestors. The procedure to achieve this is as follows.
This procedure begins by first going to the left subtree of the head node using the statement
p = root -> leftchild ;
Then through a while loop we follow the leftmost pointers until a thread to a predecessor is found. On encountering this thread we print the data for the leftmost node. Next, through another while loop we check the boolean value of the right thread. If this value is true, we follow the thread back up to the ancestor node, print this ancestor node's data. This way we continue to move up till the right thread is true. When the right thread is found to be false we again proceed by going to the right child and checking it left subtree.
As we follow these steps we are sometimes likely to reach the head node, and that is the time to stop the procedure. This is what is being achieved by the statements,
if ( p == root ) break ;

