Deletion From A Binary Tree

Deletion From A Binary Tree

In addition to techniques for inserting data in a binary tree and traversing the tree, practical examples call for deleting data from the binary tree. Assuming that we will pass the specified data item that we wish to delete to the delete( ) function, there are four possible cases that we need to consider:

1. No node in the tree contains the specified data.

2. The node containing the data has no children.

3. The node containing the data has exactly one child.

4. The node containing the data has two children.

For case (a) we merely need to print the message that the data item is not present in the tree. In case (b) since the node to be deleted has no children the memory occupied by this should be freed and either the left link or the right link of the parent of this node should be set to NULL . Which of these to set to NULL depends upon whether the node being deleted is a left child or a right child of its parent. In case (c) since the node to be deleted has one child the solution is again rather simple. We have to adjust the pointer of the parent of the node to be deleted such that after deletion it points to the child of the node being deleted. This is illustrated in Figure 7. For case (d) in which the node to be deleted has two children the solution is more complex. Consider node C in Figure 7. Before Deletion. From the figure the inorder successor of the node C is node J. The data of this inoder successor should now be copied into the node to be deleted and a pointer should be setup to the inorder successor (node J). This inorder successor would have one or zero children. This node should then be deleted using the same procedure as for deleting a one child or a zero child node. Thus the whole logic of deleting a node with two children is to locate the inorder successor, copy its data and reducing the problem to a simple deletion of a node with one or zero children. A program to implement this deletion procedure is given below.

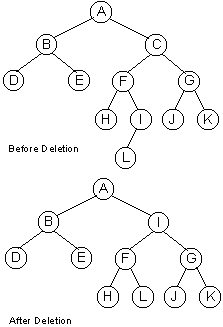
Figure 7.

 

/* Program to to delete a node form a binary search tree */

#include "alloc.h"

#define TRUE 1

#define FALSE 0

 

struct btreenode

{

struct btreenode *leftchild ;

int data ;

struct btreenode *rightchild ;

} ;

main( )

{

struct btreenode *bt ;

int req, i = 0, num, a[ ]= { 11, 9, 13, 8, 10, 12, 14, 15, 7 } ;

bt = NULL ;/* empty tree */

clrscr( ) ;

while ( i <= 8 )

{

insert ( &bt, a[i] ) ;

i++ ;

}

clrscr( ) ;

printf ( "Binary tree before deletion: " ) ;

inorder ( bt ) ;

delete ( &bt, 10 ) ;

printf ( "\nBinary tree after deletion: " ) ;

inorder ( bt ) ;

delete ( &bt, 14 ) ;

printf ( "\nBinary tree after deletion: " ) ;

inorder ( bt ) ;

delete ( &bt, 8 ) ;

printf ( "\nBinary tree after deletion: " ) ;

inorder ( bt ) ;

delete ( &bt, 13 ) ;

printf ( "\nBinary tree after deletion: " ) ;

inorder ( bt ) ;

}

 

/* inserts a new node in a binary search tree */

insert ( struct btreenode **sr, int num )

{

if ( *sr == NULL )

{

*sr = malloc ( sizeof ( struct btreenode ) ) ;

( *sr ) -> leftchild = NULL ;

( *sr ) -> data = num ;

( *sr ) -> rightchild = NULL ;

return ;

}

else /* search the node to which new node will be attached */

{

/* if new data is less, traverse to left */

if ( num < ( *sr ) -> data )

insert ( &( ( *sr ) -> leftchild ), num ) ;

else

/* else traverse to right */

insert ( &( ( *sr ) -> rightchild ), num ) ;

}

return ;

}

/* deletes a node from the binary search tree */

delete ( struct btreenode **root, int num )

{

int found ;

struct btreenode *parent, *x, *xsucc ;

/* if tree is empty */

if ( *root == NULL )

{

printf ( "\nTree is empty" ) ;

return ;

}

parent = x = NULL ;

/* call to search function to find the node to be deleted */

search ( root, num, &parent, &x, &found ) ;

/* if the node to deleted is not found */

if ( found == FALSE )

{

printf ( "\nData to be deleted, not found" ) ;

return ;

}

/* if the node to be deleted has two children */

if ( x -> leftchild != NULL && x -> rightchild != NULL)

{

parent = x ;

xsucc = x -> rightchild ;

while ( xsucc -> leftchild != NULL )

{

parent = xsucc ;

xsucc = xsucc -> leftchild ;

}

x -> data = xsucc -> data ;

x = xsucc ;

}

/* if the node to be deleted has no child */

if ( x -> leftchild == NULL && x -> rightchild == NULL )

{

if ( parent -> rightchild == x )

parent -> rightchild = NULL ;

else

parent -> leftchild = NULL ;

free ( x ) ;

return ;

}

/* if the node to be deleted has only rightchild */

if ( x -> leftchild == NULL && x -> rightchild != NULL )

{

if ( parent -> leftchild == x )

parent -> leftchild = x -> rightchild ;

else

parent -> rightchild = x -> rightchild ;

free ( x ) ;

return ;

}

/* if the node to be deleted has only left child */

if ( x -> leftchild != NULL && x -> rightchild == NULL )

{

if ( parent -> leftchild == x )

parent -> leftchild = x -> leftchild ;

else

parent -> rightchild = x -> leftchild ;

free ( x ) ;

return ;

}

}

/* returns the address of the node to be deleted, address of its parent and whether the node is found or not */

search ( struct btreenode **root, int num, struct btreenode **par, struct btreenode **x, int *found )

{

struct btreenode *q ;

q = *root ;

*found = FALSE ;

*par = NULL ;

while ( q != NULL )

{

/* if the node to be deleted is found */

if ( q -> data == num )

{

*found = TRUE ;

*x = q ;

return ;

}

if ( q -> data > num )

{

*par = q ;

q = q -> leftchild ;

}

else

{

*par = q ;

q = q -> rightchild ;

}

}

}

/* traverse a binary search tree in a LDR (Left-Data-Right) fashion */

inorder ( struct btreenode *sr )

{

if ( sr != NULL )

{

inorder ( sr -> leftchild ) ;

/* print the data of the node whose leftchild is NULL or the path has already been traversed */

printf ( "%d ", sr -> data ) ;

inorder ( sr -> rightchild ) ;

}

else

return ;

}