Conditional Probability

The conditional probability of an event B is the probability that the event will occur given the knowledge that an event A has already occurred. This probability is written P(B|A), notation for the probability of B given A. In the case where events A and B are independent (where event A has no effect on the probability of event B), the conditional probability of event B given event A is simply the probability of event B, that is P(B).

If events A and B are not independent, then the probability of the intersection of A and B (the probability that both events occur) is defined by

P(A and B) = P(A)P(B|A).

From this definition, the conditional probability P(B|A) is easily obtained by dividing by P(A):

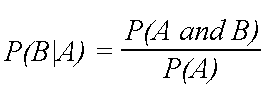
Examples

In a card game, suppose a player needs to draw two cards of the same suit in order to win. Of the 52 cards, there are 13 cards in each suit. Suppose first the player draws a heart. Now the player wishes to draw a second heart. Since one heart has already been chosen, there are now 12 hearts remaining in a deck of 51 cards. So the conditional probability P(Draw second heart|First card a heart) = 12/51. Suppose an individual applying to a college determines that he has an 80% chance of being accepted, and he knows that dormitory housing will only be provided for 60% of all of the accepted students. The chance of the student being accepted and receiving dormitory housing is defined by

P(Accepted and Dormitory Housing) = P(Dormitory Housing|Accepted)P(Accepted) = (0.60)*(0.80) = 0.48.

To calculate the probability of the intersection of more than two events, the conditional probabilities of all of the preceding events must be considered. In the case of three events, A, B, and C, the probability of the intersection P(A and B and C) = P(A)P(B|A)P(C|A and B).

Consider the college applicant who has determined that he has 0.80 probability of acceptance and that only 60% of the accepted students will receive dormitory housing. Of the accepted students who receive dormitory housing, 80% will have at least one roommate. The probability of being accepted and receiving dormitory housing and having no roommates is calculated by: P(Accepted and Dormitory Housing and No Roommates) = P(Accepted)P(Dormitory Housing|Accepted)P(No Roomates|Dormitory Housing and Accepted) = (0.80)*(0.60)*(0.20) = 0.096. The student has about a 10% chance of receiving a single room at the college.

Another important method for calculating conditional probabilities is given by Bayes's formula. The formula is based on the expression P(B) = P(B|A)P(A) + P(B|Ac)P(Ac), which simply states that the probability of event B is the sum of the conditional probabilities of event B given that event A has or has not occurred. For independent events A and B, this is equal to P(B)P(A) + P(B)P(Ac) = P(B)(P(A) + P(Ac)) = P(B)(1) = P(B), since the probability of an event and its complement must always sum to 1. Bayes's formula is defined as follows:

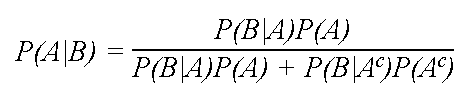
Example

Suppose a voter poll is taken in three states. In state A, 50% of voters support the liberal candidate, in state B, 60% of the voters support the liberal candidate, and in state C, 35% of the voters support the liberal candidate. Of the total population of the three states, 40% live in state A, 25% live in state B, and 35% live in state C. Given that a voter supports the liberal candidate, what is the probability that she lives in state B? By Bayes's formula,

P(Voter lives in state B|Voter supports liberal candidate) =
P(Voter supports liberal candidate|Voter lives in state B)P(Voter lives in state B)/
(P(Voter supports lib. cand.|Voter lives in state A)P(Voter lives in state A) +
P(Voter supports lib. cand.|Voter lives in state B)P(Voter lives in state B) +
P(Voter supports lib. cand.|Voter lives in state C)P(Voter lives in state C))
= (0.60)*(0.25)/((0.50)*(0.40) + (0.60)*(0.25) + (0.35)*(0.35))
= (0.15)/(0.20 + 0.15 + 0.1225) = 0.15/0.4725 = 0.3175.