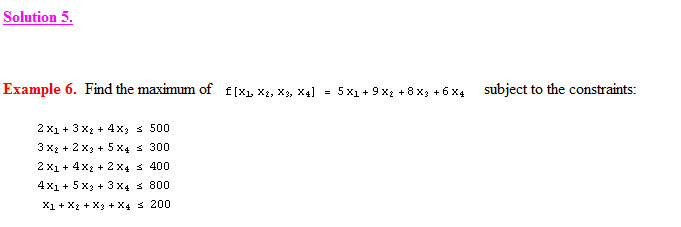Linear Programming-Simplex Method

Linear programming structure: It has an objective function with constraints on that function.

Linear function: It represents a function in which each variable is single and continuous that is raised to power 1.

Objective function:The linear function to be maximized or minimized is called an objective function.

Decision variables: Decision variables are represented the economic or physical quantities that are competing with one another for sharing the given limited resources.

Constraints: Constraints represent the limitations of the resources such as labor, time, capacity, raw materials, space etc., These constraints must be capable of expressed in the form linear equalities ( =) or in equalities ( ≤or ≥ ) in terms of decision variables.

Feasible solutions:Feasible solutions are the values of decisions variables that satisfy the given constrains for a set of variables’ solution is called as feasible region.

Feasible region: The collection of all feasible solutions.

Optimal solution: Among the many feasible solutions, a solution which optimizes the objective is called as optimal solution.

Assumptions of linear programming : A problem can be represented as a linear program if the following assumptions hold:

The constraints and objective function must be linear. Linearity requires the following

a. Proportionality:A change in a variable results in the proportionate change in the contribution of the variable to the value of the function.

b. Additive:it means there can not be any interactions between the effects of different level of activities. Eg. The level of activity X1.

should not affect the effects ( cost or benefits) of the level of activity X2.

2. Divisibility: It indicates that the numerical values of the decision variables are continues (fractional values) and are not restricted to integers.Integer Programming may be used if the values of decision variables make sense if they are integers.