Stacks and Queues

Two of the more common data objects found in computer algorithms are stacks and queues. Both of these objects are special cases of the more general data object, an ordered list.

A stack is an ordered list in which all insertions and deletions are made at one end, called the top. A queue is an ordered list in which all insertions take place at one end, the rear, while all deletions take place at the other end, the front. Given a stack S=(a[1],a[2],.......a[n]) then we say that a1 is the bottommost element and element a[i]) is on top of element a[i-1], 1<i<=n. When viewed as a queue with a[n] as the rear element one says that a[i+1] is behind a[i], 1<i<=n.

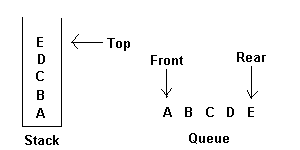
The restrictions on a stack imply that if the elements A,B,C,D,E are added to the stack, n that order, then th efirst element to be removed/deleted must be E. Equivalently we say that the last element to be inserted into the stack will be the first to be removed. For this reason stacks are sometimes referred to as Last In First Out (LIFO) lists. The restrictions on queue imply that the first element which is inserted into the queue will be the first one to be removed. Thus A is the first letter to be removed, and queues are known as First In First Out (FIFO) lists. Note that the data object queue as defined here need not necessarily correspond to the mathemathical concept of queue in which the insert/delete rules may be different

You can see the algorithms you want by clicking on the items below:

• Adding an element into a stack.
• Deleting an element from a stack.
• Adding an element into a queue.
• Deleting an element from a queue.

Adding into stack

procedure add(item : items);
{add item to the global stack stack;
top is the current top of stack
and n is its maximum size}
begin
   if top = n then stackfull;
   top := top+1;
   stack(top) := item;
end: {of add}

Deletion in stack

procedure delete(var item : items);
{remove top element from the stack stack and put it in the item}
begin
   if top = 0 then stackempty;
   item := stack(top);
   top := top-1;
end; {of delete}
These two procedures are so simple that they perhaps need no more explanation. Procedure delete actually combines the functions TOP and DELETE, stackfull and stackempty are procedures which are left unspecified since they will depend upon the particular application. Often a stackfull condition will signal that more storage needs to be allocated and the program re-run. Stackempty is often a meaningful condition.

Addition into a queue

procedure addq (item : items);
{add item to the queue q}
begin
   if rear=n then queuefull
   else begin
      rear :=rear+1;
      q[rear]:=item;
   end;
end;{of addq}

Deletion in a queue

procedure deleteq (var item : items);
{delete from the front of q and put into item}
begin
   if front = rear then queueempty
   else begin
      front := front+1
      item := q[front];
   end;
end; {of deleteq}