Hashing, Hash Data Structure and Hash Table

Hashing is the process of mapping large amount of data item to a smaller table with the help of a hashing function. The essence of hashing is to facilitate the next level searching method when compared with the linear or binary search. The advantage of this searching method is its efficiency to hand vast amount of data items in a given collection (i.e. collection size).

Due to this hashing process, the result is a Hash data structure that can store or retrieve data items in an average time disregard to the collection size.

Hash Table is the result of storing the hash data structure in a smaller table which incorporates the hash function within itself. The Hash Function primarily is responsible to map between the original data item and the smaller table itself. Here the mapping takes place with the help of an output integer in a consistent range produced when a given data item (any data type) is provided for storage and this output integer range determines the location in the smaller table for the data item. In terms of implementation, the hash table is constructed with the help of an array and the indices of this array are associated to the output integer range.

Hash Table Example

Here, we construct a hash table for storing and retrieving data related to the citizens of a county and the social-security number of citizens are used as the indices of the array implementation (i.e. key). Let's assume that the table size is 12, therefore the hash function would be Value modulus of 12.

Hence, the Hash Function would equate to:

(sum of numeric values of the characters in the data item) %12

Note! % is the modulus operator

Let us consider the following social-security numbers and produce a hashcode:

120388113D => 1+2+0+3+8+8+1+1+3+13=40
Hence, (40)%12 => Hashcode=4

310181312E => 3+1+0+1+8+1+3+1+2+14=34
Hence, (34)%12 => Hashcode=10

041176438A => 0+4+1+1+7+6+4+3+8+10=44
Hence, (44)%12 => Hashcode=8

Therefore, the Hashtable content would be as follows:
-----------------------------------------------------
0:empty
1:empty
2:empty
3:empty
4:occupied Name:Drew Smith SSN:120388113D
5:empty
6:empty
7:empty
8:occupied Name:Andy Conn SSN:041176438A
9:empty
10:occupied Name:Igor Barton SSN:310181312E
11:empty

Direct Address Tables

If we have a collection of n elements whose keys are unique integers in (1,m), where m >= n, then we can store the items in a direct address table, T[m], where Ti is either empty or contains one of the elements of our collection. Searching a direct address table is clearly an O(1) operation: for a key, k, we access Tk,

• if it contains an element, return it,
• if it doesn't then return a NULL.

1. the keys must be unique, and
2. the range of the key must be severely bounded.

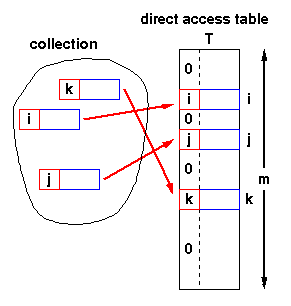
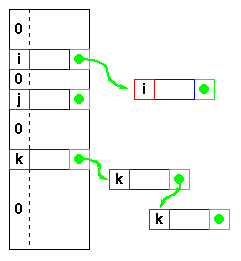
If the keys are not unique, then we can simply construct a set of m lists and store the heads of these lists in the direct address table. The time to find an element matching an input key will still be O(1).
However, if each element of the collection has some other distinguishing feature (other than its key), and if the maximum number of duplicates is ndupmax, then searching for a specific element is O(ndupmax). If duplicates are the exception rather than the rule, then ndupmax is much smaller than n and a direct address table will provide good performance. But if ndupmax approaches n, then the time to find a specific element is O(n) and a tree structure will be more efficient.

The range of the key determines the size of the direct address table and may be too large to be practical. For instance it's not likely that you'll be able to use a direct address table to store elements which have arbitrary 32-bit integers as their keys for a few years yet!
Direct addressing is easily generalised to the case where there is a function,

h(k) => (1,m)

which maps each value of the key, k, to the range (1,m). In this case, we place the element in T[h(k)] rather than T[k] and we can search in O(1) time as before.

Mapping functions

The direct address approach requires that the function, h(k), is a one-to-one mapping from each k to integers in (1,m). Such a function is known as a perfect hashing function: it maps each key to a distinct integer within some manageable range and enables us to trivially build an O(1) search time table.
Unfortunately, finding a perfect hashing function is not always possible. Let's say that we can find a hash function, h(k), which maps most of the keys onto unique integers, but maps a small number of keys on to the same integer. If the number of collisions (cases where multiple keys map onto the same integer), is sufficiently small, then hash tables work quite well and give O(1) search times.

Handling the collisions

In the small number of cases, where multiple keys map to the same integer, then elements with different keys may be stored in the same "slot" of the hash table. It is clear that when the hash function is used to locate a potential match, it will be necessary to compare the key of that element with the search key. But there may be more than one element which should be stored in a single slot of the table. Various techniques are used to manage this problem:

• chaining,
• overflow areas,
• re-hashing,
• using neighbouring slots (linear probing),
• quadratic probing,
• random probing, ...

Chaining

One simple scheme is to chain all collisions in lists attached to the appropriate slot. This allows an unlimited number of collisions to be handled and doesn't require a priori knowledge of how many elements are contained in the collection. The tradeoff is the same as with linked lists versus array implementations of collections: linked list overhead in space and, to a lesser extent, in time.

Re-hashing

Re-hashing schemes use a second hashing operation when there is a collision. If there is a further collision, we re-hash until an empty "slot" in the table is found.

The re-hashing function can either be a new function or a re-application of the original one. As long as the functions are applied to a key in the same order, then a sought key can always be located.

Linear probing

One of the simplest re-hashing functions is +1 (or -1), ie on a collision, look in the neighbouring slot in the table. It calculates the new address extremely quickly and may be extremely efficient on a modern RISC processor due to efficient cache utilisation (cf. the discussion of linked list efficiency). The animation gives you a practical demonstration of the effect of linear probing: it also implements a quadratic re-hash function so that you can compare the difference.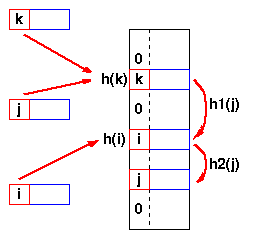

Clustering

Linear probing is subject to a clustering phenomenon. Re-hashes from one location occupy a block of slots in the table which "grows" towards slots to which other keys hash. This exacerbates the collision problem and the number of re-hashed can become large. Quadratic Probing
Better behaviour is usually obtained with quadratic probing, where the secondary hash function depends on the re-hash index:
address = h(key) + c i2
on the tth re-hash. (A more complex function of i may also be used.) Since keys which are mapped to the same value by the primary hash function follow the same sequence of addresses, quadratic probing shows secondary clustering. However, secondary clustering is not nearly as severe as the clustering shown by linear probes. Re-hashing schemes use the originally allocated table space and thus avoid linked list overhead, but require advance knowledge of the number of items to be stored.
However, the collision elements are stored in slots to which other key values map directly, thus the potential for multiple collisions increases as the table becomes full.

Overflow area

Another scheme will divide the pre-allocated table into two sections: the primary area to which keys are mapped and an area for collisions, normally termed the overflow area.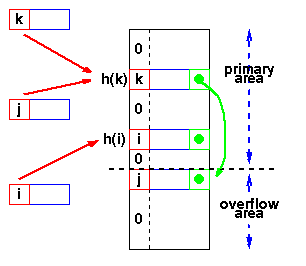

When a collision occurs, a slot in the overflow area is used for the new element and a link from the primary slot established as in a chained system. This is essentially the same as chaining, except that the overflow area is pre-allocated and thus possibly faster to access. As with re-hashing, the maximum number of elements must be known in advance, but in this case, two parameters must be estimated: the optimum size of the primary and overflow areas.
Of course, it is possible to design systems with multiple overflow tables, or with a mechanism for handling overflow out of the overflow area, which provide flexibility without losing the advantages of the overflow scheme.