Merge Sort

MergeSort is a Divide and Conquer algorithm. It divides input array in two halves, calls itself for the two halves and then merges the two sorted halves. The merg() function is used for merging two halves. The merge(arr, l, m, r) is key process that assumes that arr[l..m] and arr[m+1..r] are sorted and merges the two sorted sub-arrays into one. See following C implementation for details.

MergeSort(arr[], l, r)
If r > l
    1. Find the middle point to divide the array into two halves:
        middle m = (l+r)/2
   2. Call mergeSort for first half:
       Call mergeSort(arr, l, m)
   3. Call mergeSort for second half:
       Call mergeSort(arr, m+1, r)
   4. Merge the two halves sorted in step 2 and 3:
       Call merge(arr, l, m, r)

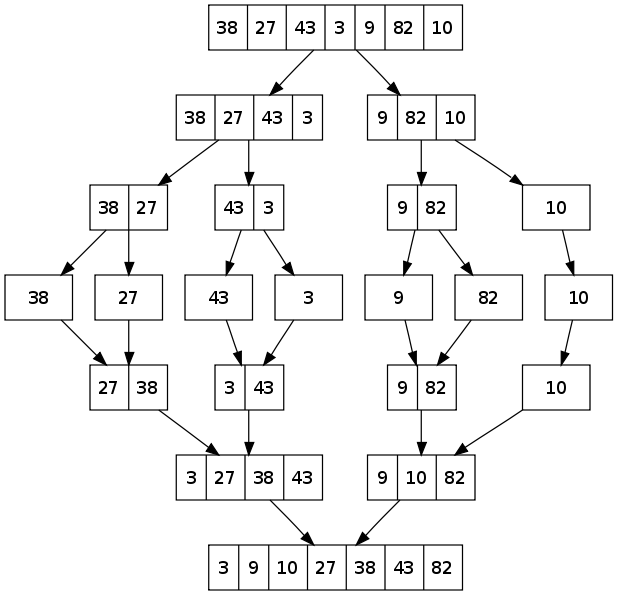
The following diagram from wikipedia shows the complete merge sort process for an example array {38, 27, 43, 3, 9, 82, 10}. If we take a closer look at the diagram, we can see that the array is recursively divided in two halves till the size becomes 1. Once the size becomes 1, the merge processes comes into action and starts merging arrays back till the complete array is merged.



/* C program for merge sort */ #include<stdlib.h> #include<stdio.h> /* Function to merge the two haves arr[l..m] and arr[m+1..r] of array arr[] */
void merge(int arr[], int l, int m, int r)
{
   int i, j, k;
   int n1 = m - l + 1;
   int n2 = r - m;
   /* create temp arrays */
   int L[n1], R[n2];
   /* Copy data to temp arrays L[] and R[] */
   for(i = 0; i < n1; i++)
      L[i] = arr[l + i];
   for(j = 0; j < n2; j++)
      R[j] = arr[m + 1+ j];

   /* Merge the temp arrays back into arr[l..r]*/
   i = 0;
   j = 0;
   k = l;
   while (i < n1 && j < n2)

   {       if (L[i] <= R[j])
      {
         arr[k] = L[i];
         i++;
      }
      else
      {
         arr[k] = R[j];
         j++;
      }
      k++;
   }

   /* Copy the remaining elements of L[], if there are any */v    while (i < n1)
   {
      arr[k] = L[i];
      i++;
      k++;
   }

   /* Copy the remaining elements of R[], if there are any */
   while (j < n2)
   {
      arr[k] = R[j];
      j++;
      k++;
   }
}

   /* l is for left index and r is right index of the sub-arrayv    of arr to be sorted */
   void mergeSort(int arr[], int l, int r)
   {
      if (l < r)
      {
      int m = l+(r-l)/2; //Same as (l+r)/2, but avoids overflow for large l and h
      mergeSort(arr, l, m);
       mergeSort(arr, m+1, r);
      merge(arr, l, m, r);
      }
}
    /* UITLITY FUNCTIONS */
/* Function to print an array */
void printArray(int A[], int size)
{
    int i;
    for (i=0; i < size; i++)
       printf("%d ", A[i]);
   printf("\n");
}

/* Driver program to test above functions */ int main()
{    int arr[] = {12, 11, 13, 5, 6, 7};
   int arr_size = sizeof(arr)/sizeof(arr[0]);

   printf("Given array is \n");
   printArray(arr, arr_size);

   mergeSort(arr, 0, arr_size - 1);

   printf("\nSorted array is \n");
   printArray(arr, arr_size);
   return 0;

Output:
Given array is
12   11   13   5   6   7

Sorted array is
5   6   7   11   12   13

Time Complexity: Sorting arrays on different machines. Merge Sort is a recursive algorithm and time complexity can be expressed as following recurrence relation.

T(n) = 2T(n/2) + \Theta(n)

The above recurrence can be solved either using Recurrence Tree method or Master method. It falls in case II of Master Method and solution of the recurrence is \Theta(nLogn).

Time complexity of Merge Sort is \Theta(nLogn) in all 3 cases (worst, average and best) as merge sort always divides the array in two halves and take linear time to merge two halves.

Auxiliary Space: O(n)

Algorithmic Paradigm: Divide and Conquer

Sorting In Place: No in a typical implementation

Stable: Yes

Applications of Merge Sort
1) Merge Sort is useful for sorting linked lists in O(nLogn) time. Other nlogn algorithms like Heap Sort, Quick Sort (average case nLogn) cannot be applied to linked lists.
2) Inversion Count Problem
3) Used in External Sorting