Depth First Traversal for a Graph

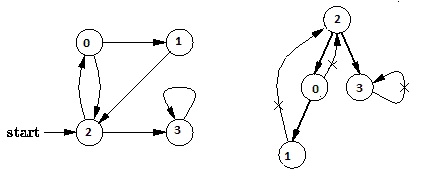
Depth First Traversal (or Search) for a graph is similar to Depth First Traversal of a tree. The only catch here is, unlike trees, graphs may contain cycles, so we may come to the same node again. To avoid processing a node more than once, we use a boolean visited array. For example, in the following graph, we start traversal from vertex 2. When we come to vertex 0, we look for all adjacent vertices of it. 2 is also an adjacent vertex of 0. If we don’t mark visited vertices, then 2 will be processed again and it will become a non-terminating process. Depth First Traversal of the following graph is 2, 0, 1, 3

Following is C++ implementation of simple Depth First Traversal. The implementation uses adjacency list representation of graphs. STL‘s list container is used to store lists of adjacent nodes.

#include<iostream>
#include

using namespace std;

// Graph class represents a directed graph using adjacency list representation
class Graph
{
   int V; // No. of vertices
   list<int> *adj; // Pointer to an array containing adjacency lists
   void DFSUtil(int v, bool visited[]); // A function used by DFS
public:
   Graph(int V); // Constructor
   void addEdge(int v, int w); // function to add an edge to graph
   void DFS(int v); // DFS traversal of the vertices reachable from v
};

Graph::Graph(int V)
{
   this->V = V;
   adj = new list[V];
}

void Graph::addEdge(int v, int w)
{
   adj[v].push_back(w); // Add w to v’s list.
}

void Graph::DFSUtil(int v, bool visited[])
{
// Mark the current node as visited and print it
visited[v] = true;
cout << v << " ";

// Recur for all the vertices adjacent to this vertex
list<int>::iterator i;
for(i = adj[v].begin(); i != adj[v].end(); ++i)
if(!visited[*i])
DFSUtil(*i, visited);
}

// DFS traversal of the vertices reachable from v. It uses recursive DFSUtil()
void Graph::DFS(int v)
{
// Mark all the vertices as not visited
bool *visited = new bool[V];
for(int i = 0; i < V; i++)
visited[i] = false;

// Call the recursive helper function to print DFS traversal
DFSUtil(v, visited);
}

int main()
{
// Create a graph given in the above diagram
   Graph g(4);
   g.addEdge(0, 1);
   g.addEdge(0, 2);
   g.addEdge(1, 2);
   g.addEdge(2, 0);
   g.addEdge(2, 3);
   g.addEdge(3, 3);

   cout << "Following is Depth First Traversal (starting from vertex 2) \n";
   g.DFS(2);

return 0;
}

Output:
Following is Depth First Traversal (starting from vertex 2)
2 0 1 3

Note that the above code traverses only the vertices reachable from a given source vertex. All the vertices may not be reachable from a given vertex (example Disconnected graph). To do complete DFS traversal of such graphs, we must call DFSUtil() for every vertex. Also, before calling DFSUtil(), we should check if it is already printed by some other call of DFSUtil(). Following implementation does the complete graph traversal even if the nodes are unreachable. The differences from the above code are highlighted in the below code.

#include<iostream>
#include <list>
using namespace std;

class Graph
{
int V; // No. of vertices
list<int> *adj; // Pointer to an array containing adjacency lists
void DFSUtil(int v, bool visited[]); // A function used by DFS
public:
Graph(int V); // Constructor
void addEdge(int v, int w); // function to add an edge to graph
void DFS(); // prints DFS traversal of the complete graph
};

Graph::Graph(int V)
{
this->V = V;
adj = new list<int>[V];
}

void Graph::addEdge(int v, int w)
{
adj[v].push_back(w); // Add w to v’s list.
}

void Graph::DFSUtil(int v, bool visited[])
{
// Mark the current node as visited and print it
visited[v] = true;
cout << v << " ";

// Recur for all the vertices adjacent to this vertex
list<int>::iterator i;
for(i = adj[v].begin(); i != adj[v].end(); ++i)
if(!visited[*i])
DFSUtil(*i, visited);
}

// The function to do DFS traversal. It uses recursive DFSUtil()
void Graph::DFS()
{
// Mark all the vertices as not visited
bool *visited = new bool[V];
for(int i = 0; i < V; i++)
visited[i] = false;

// Call the recursive helper function to print DFS traversal
// starting from all vertices one by one
for(int i = 0; i < V; i++)
if(visited[i] == false)
DFSUtil(i, visited);
}

int main()
{
// Create a graph given in the above diagram
Graph g(4);
g.addEdge(0, 1);
g.addEdge(0, 2);
g.addEdge(1, 2);
g.addEdge(2, 0);
g.addEdge(2, 3);
g.addEdge(3, 3);

cout << "Following is Depth First Traversal (starting from vertex 0) \n";
g.DFS();

return 0;
}
Time Complexity: O(V+E) where V is number of vertices in the graph and E is number of edges in the graph.